Ce cours vous apprendra les concepts de base des vecteurs, notamment leur définition et les différentes opérations possibles. Vous mettrez ensuite ces concepts en pratique en développant un mini-jeu vidéo où un avion pourra se déplacer dans toutes les directions grâce aux touches fléchées du clavier de votre PC.
Ce premier mini-jeu vidéo nécessite de calculer les coordonnées d'un vecteur pour déplacer l'avion sur l'écran lorsque les touches fléchées du clavier sont utilisées. Pour cela, nous utiliserons la fonction PVector de la bibliothèque mathématique de p5.js. Nous examinerons tout cela en détail sous la rubrique « Algorithme » située dans la barre de menus.
Un bipoint (ou une flèche) est un segment orienté. C'est un segment auquel s'ajoute l'information sens. Ainsi pour 2 points A et B,
le bipoint (A,B) est différent du bipoint (B,A) car ils n'ont pas le même sens. (respectivement de A vers B et de B vers A). Une direction est un ensemble de toutes les
droites parallèles entre elles. Un vecteur AB→ est défini par :
Sa direction : celle de la droite (AB)
Son sens : il va de A vers B.
Sa norme, notée ||AB||→, représente la longueur du segment AB.
Note : En physique, des quantités comme l'aire, le volume, la longueur, la température et le temps n'ont qu'une intensité et peuvent être entièrement représentées par un nombre réel (accompagné de l'unité de mesure adéquate, cm², m³, cm, ° ou s). Une grandeur de ce type est une grandeur scalaire et le nombre réel correspondant est un scalaire. Des concepts tels que les vitesses ou les forces ont à la fois une intensité, un sens et une direction et sont souvent représentés par un segment de droite orienté, C'est-à-dire un segment de droite avec une direction propre et un sens. On nomme aussi ce segment de droite orienté un vecteur. Comme le montre la figure ci-dessous, nous utilisons AB→ pour désigner le vecteur dont l'origine est A et l'extrémité B et nous indiquons le sens du vecteur en traçant une flèche dirigée de A vers B dont la pointe est au point B. La norme (ou intensité) de AB→ est la longueur du segment (AB) et est notée par ||AB||→. Comme sur la figure, nous utilisons la notation u→ ou v→ pour désigner des vecteurs dont les extrémités ne sont pas spécifiées.
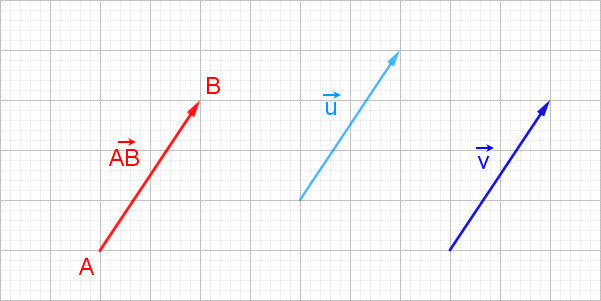
Note : Nous verrons, au cours de ce chapitre, des vecteurs qui se présentent dans un plan. Nous pouvons donc également les nommer vecteurs de dimension 2.
En géométrie classique, un plan est une surface plate illimitée, munie de notions d’alignement, d’angle et de distance, et dans laquelle peuvent s’inscrire des points, droites, cercles et autres figures planes usuelles. Il sert ainsi de cadre à la géométrie plane, et en particulier à la trigonométrie lorsqu’il est muni d’une orientation, et permet de représenter l’ensemble des nombres complexes.
Techniquement parlant, la définition d'un vecteur est la différence entre deux points. Réfléchissez comment vous pourriez aller d'un point A à un point B en suivant
des instructions sur une carte géographique aux points cardinaux, Nord, Sud, Est et Ouest.
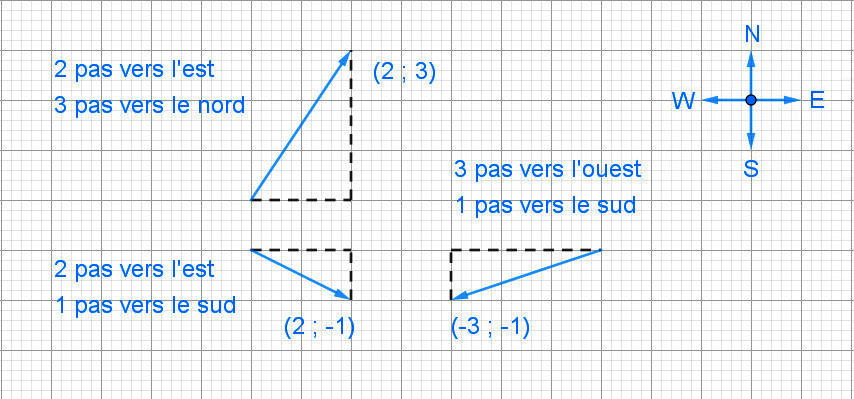
Soit (O, I, J) un repère du plan et u→ un vecteur dont un représentant est AB→.
Pour lire les coordonnées du vecteur u→, on décompose la translation qui transforme A en B, c'est-à-dire
la translation de vecteur u→, en deux translations successives : d'abord une translation parallèlement à l'axe (OI),
puis une translation parallèlement à l'axe (OJ).
Le déplacement parallèlement à (OI) donne l'abscisse du vecteur :
Si ce déplacement s'effectue dans le sens des x croissants (de O vers I), il est compté positivement.
Si ce déplacement s'effectue dans le sens des x décroissants (de I vers O), il est compté négativement.
Le déplacement parallèlement à (OJ) donne l'ordonnée du vecteur :
Si ce déplacement s'effectue dans le sens des y croissants (de O vers J), il est compté positivement.
Si ce déplacement s'effectue dans le sens des y décroissants (de J vers O), il est compté négativement.
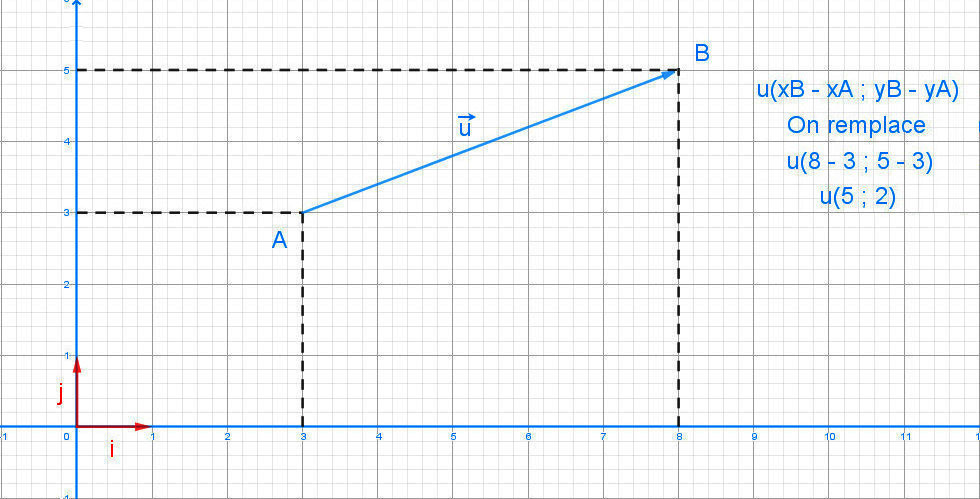
Par exemple , pour aller de A à B, on se déplace parallèlement à (OI) de 5 unités dans le sens des x croissants.
l'abscisse du vecteur u→ est donc +5.
On se déplace ensuite parallèlement à (OJ) de 2 unités dans le sens des y croissants.
l'ordonnée du vecteur u→ est donc +2.
Le vecteur u→ a donc pour coordonnées (5 ; 2). On note alors u→(5; 2).
On peut vérifié notre calcul en faisant : u→=(xB-xA; yB-yA) pour l'abscisse et l'ordonnée.
On remplace u→ = (8 - 3 ; 5 - 3) ⇔ u→ = (+5 ; +2).
La notion de vecteur du plan se généralise sans difficulté à l’espace. Soient A et B deux points distincts de l'espace. Le vecteur AB→ est parfaitement déterminée par sa direction celle de la droite (AB), son sens de A vers B, sa norme, qui est la longueur du segment AB noté ||AB||→.
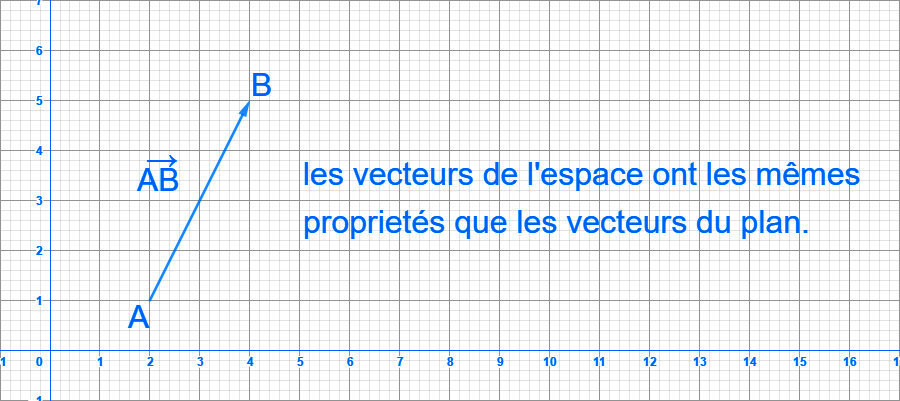
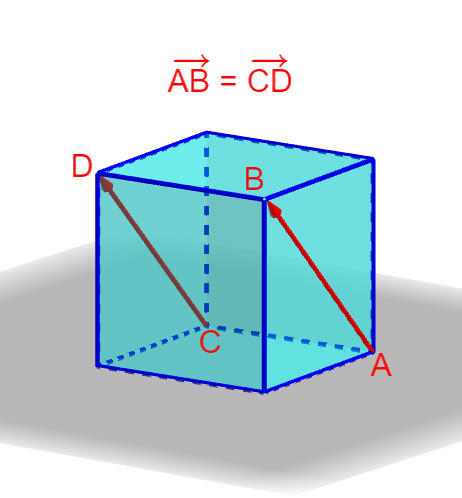
Soient A,B,C et D quatre points de l’espace. Les deux vecteurs non nuls AB→ et
CD→ sont égaux si et seulement s'ils ont même direction, même sens et même norme,
si et seulement si ABCD est parallélogramme.
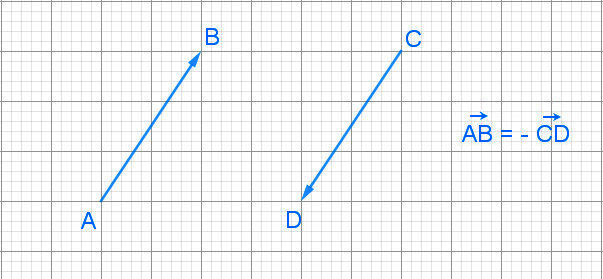
Soient A,B,C et D quatre points de l’espace. Les deux vecteurs non nuls AB→
et CD→ sont opposés si et seulement s'ils ont même direction, des sens opposés et même norme.
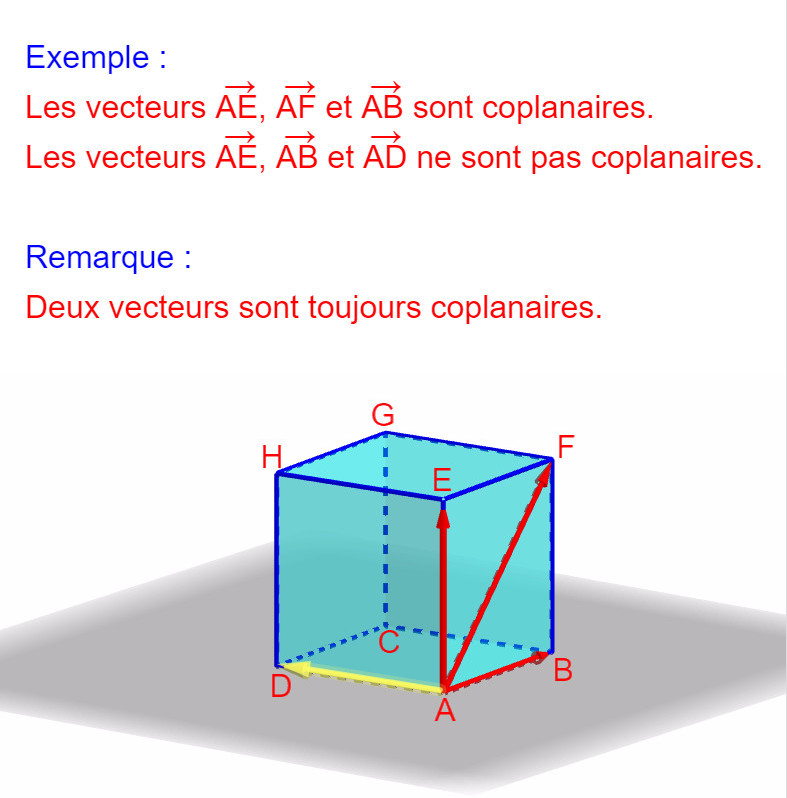
Des vecteurs sont coplanaires si et seulement en traçant leurs représentants à partir d’un même point A, les extrémités de ces représentants sont coplanaires avec A.
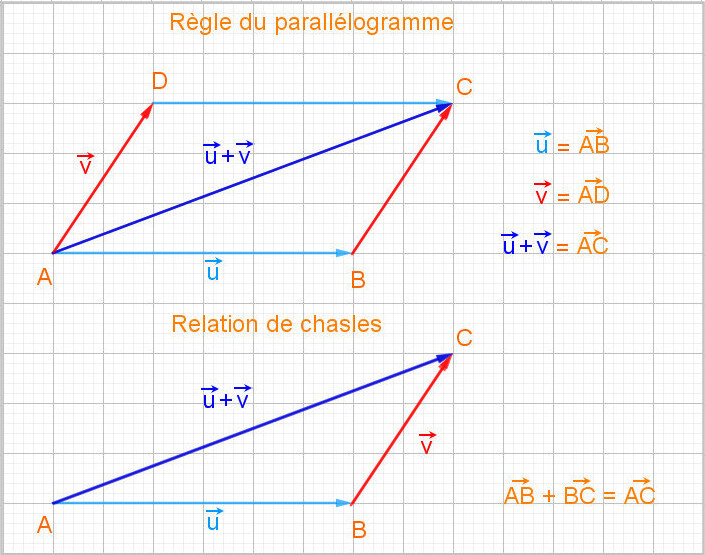
Soient u→ et v→ deux vecteurs de l’espace.
Comme les vecteurs u→ et v→ sont coplanaires,
on peut obtenir la somme de ces deux vecteurs en utilisant les deux méthodes utilisées dans le plan : la règle du parallélogramme
ou la relation de Chasles.
Article Wikipédia : règle du parallélogramme.
Article Wikipédia : relation de Chasles.
Article Wikipédia : Michel Chasles.
Soient u→ et v→ deux vecteurs de l’espace.
Comme les vecteurs u→ et v→ sont coplanaires,
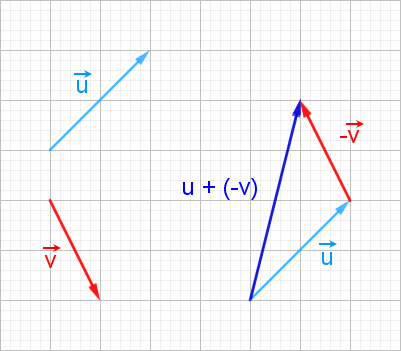
on peut soustraire ces deux vecteurs en utilisant la méthode de la relation de Chasles vu ci-dessus. Soustraire le vecteur v→
au vecteur u→, c'est ajouter à u→
l'opposé de v→ : en clair u→ - v→
= u→ + ( -v→ ).
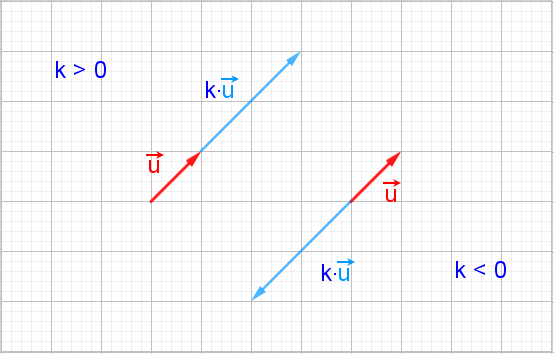
Soit u→ un vecteur de l’espace et soit k un nombre réel. On définit le vecteur k·u→ de la façon suivante :
Si k = 0 alors k·u→ = 0·u→ = 0
Si u→ = 0 alors k·u→ = 0·u→ = 0
Si k ≠ 0 et u→ ≠ 0 alors k·u→
est le vecteur qui a même direction que u→, même sens que u→
si k > 0 et sens contraire à celui de u→ si k < 0
pour norme celle de u→ multiplier par k,
||k·u→||
= k·||u→||
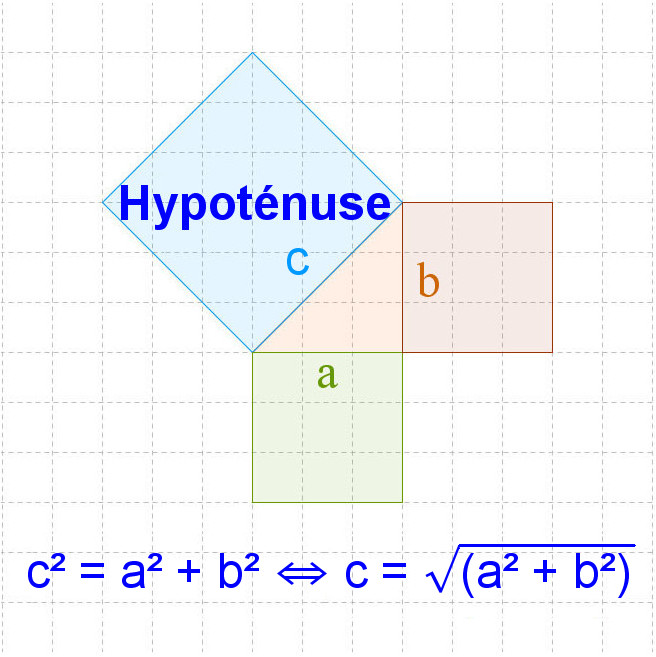
Nous pouvons trouver la norme de tout vecteur assez facilement en utilisant le théorème de Pythagore. En particulier, la longueur de l’hypoténuse est donc toujours
supérieure à celle de chaque autre côté. Le terme « longueur » est parfois omis, chaque côté étant assimilé à sa longueur. Toutefois l’élévation au carré (algébrique),
qui n’a de sens que pour une grandeur numérique comme la longueur, correspond à la construction d’un carré (géométrique) sur chaque côté du triangle. Certaines
démonstrations du théorème de Pythagore s’appuient d’ailleurs sur une égalité d’aires entre le carré construit sur l’hypoténuse et la réunion des carrés construits
sur les deux autres côtés. En nommant les sommets du triangle, le théorème de Pythagore peut se reformuler dans l’implication suivante : si un triangle abc est rectangle
en b, alors c2 = a2 + b2. Avec cela en mémoire nous pouvons jeter un regard sur le diagrame ci-dessous.
Article Wikipédia : théorème de Pythagore.
Article Wikipédia : Pythagore.
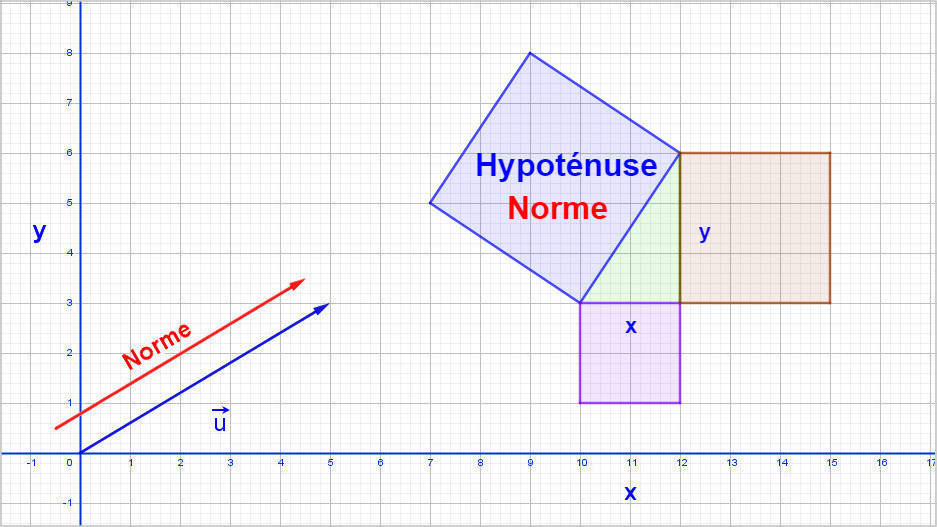
Nous voyons que dans le diagramme ci-dessus, le calcul de la norme d'un vecteur ressemble remarquablement au théorème de Pythagore, nous remplaçons donc a par x,
pour l'axe des abscisses et b par y, pour l'axe des ordonnées (voir la figure ci-dessus sur le rappel du théorème de Pythagore).
Ce qui veut dire que l'on reprend la formule du théorème de Pythagore : norme² = x² + y².
Bien entendu, nous ne voulons pas la norme élevée au carré, mais juste la norme régulière, nous éliminons donc la norme élevée au carré et prenons la racine carré des
deux autres côtés, c'est-à-dire x et y. Ce qui finalement revient à dire que la norme = √ ( x² + y² ). Maintenant vous savez tout ce qu'il faut pour calculer la norme d'un vecteur.
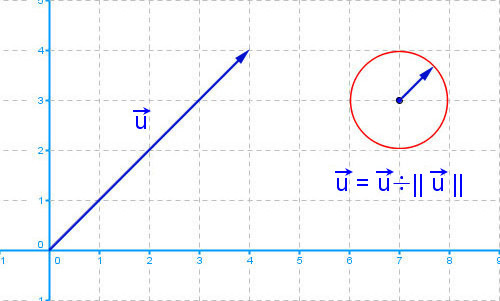
Un vecteur dont la norme est 1 est appelé un vecteur unitaire. Un vecteur dont la norme est 0 et dont le sens et la direction ne sont pas définis est appelé un vecteur nul.
On le note 0E ou 0 ou encore 0→ avec une flèche haut dessus. Pour normaliser ce vecteur, de longueur quelconque
et en le gardant pointant dans la même direction, il faut diviser ce vecteur u→ par sa norme, ce qui donne
un vecteur unitaire égal à 1.
1.Définition :
Le produit scalaire est une opération mathématique qui associe deux vecteurs u→ et v→ à un nombre (un scalaire).
Le produit scalaire est défini comme :
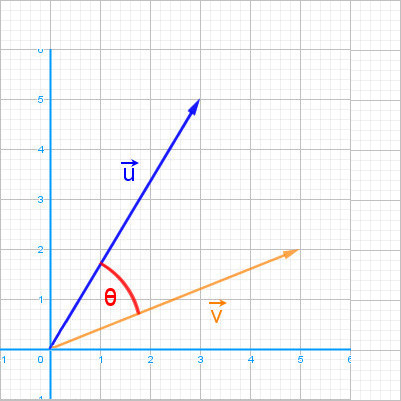
u→ · v→ = ||u→|| · ||v→|| · cos (θ)
où :
||u→|| et ||v→|| sont les normes des vecteurs u→ et v→,
θ est l'angle formé entre u→ et v→ (en radians ou degrés)
2.Propriétés du produit scalaire :
1.Symétrie :
u→ · v→ = v→ · u→
2.Orthogonalité :
Si u→ et v→ sont orthogonaux (perpendiculaires), alors :
u→ · v→ = 0
3.Calcul en coordonnées :
Si les vecteurs u→ et v→ sont donnés dans un repère orthonormé par leurs coordonnées :
u→ = (u→x, u→y, u→z) et v→ = (v→x, v→y, v→z)
le produit scalaire se calcule par :
u→ · v→ = u→x · v→x + u→y · v→y + u→z · v→z
Exemple en dimension 2 :
Si u→ = (3, 4) et v→ = (1, 2) alors :
u→ · v→ = 3 · 1 + 4 · 2 = 3 + 8 = 11
Le produit scalaire permet de mesurer la projection d’un vecteur sur un autre, de déterminer l’angle θ entre eux ou de vérifier leur orthogonalité.
Note : Nous venons de voir des vecteurs qui se présentent dans un plan avec les coordonnées {x, y}. Si nous ajoutons la coordonnée z, nous obtenons un espace avec les coordonnées {x, y, z}. Ce n'est pas plus difficile que cela : les opérations de calcul sont les mêmes avec les vecteurs de l'espace qu'avec ceux du plan, à la différence près que nous rajoutons z comme composante aux coordonnées {x, y}. Nous pouvons donc également les nommer vecteurs de dimension 3.
Article nagwa : Opérations sur les vecteurs en 3DCe cours sur les vecteurs est maintenant terminé pour la théorie mais on va le reprendre côté code avec le langage de programmation JavaScript dans l'éditeur de code de p5.js pour programmer notre premier mini-jeu vidéo sous la rubrique « Algorithme » située dans la barre de menus.