Ce cours vous permettra de maîtriser les principales fonctions trigonométriques. Vous aurez l'occasion de les appliquer dans un algorithme basé sur les théories apprises. Nous développerons également un mini-jeu vidéo où un avion ennemi descendra de haut en bas de l’écran, tirant des balles à intervalles réguliers pour viser un avion mère que vous pourrez contrôler et déplacer sur l’écran de votre PC.
Dans ce deuxième mini-jeu vidéo, nous utiliserons des calculs trigonométriques. Nous exploiterons la fonction arctan (arc tangente) des mathématiques, appelée atan dans la bibliothèque mathématique de p5.js. Je vous montrerai également, en mathématiques comment passer des coordonnées polaires aux coordonnées cartésiennes pour gérer les trajectoires des balles de l'avion ennemi visant l'avion mère. Nous utiliserons des variables simples, x et y, pour les coordonnées cartésiennes de l'avion ennemi et un vecteur PVector pour l'avion mère afin de les déplacer sur l’écran à l’aide des touches fléchées du clavier. Nous examinerons tout cela en détail dans la rubrique « Algorithme » située dans la barre de menus.
Si vous suivez le fil conducteur et vous y mettez de votre bon sens, ce cours va vous permettre d'accélérer sur la trigonométrie, alors allons-y un pas devant l'autre sans sauter les étapes et commençons !
Tout d'abord qu'est-ce que la trigonométrie ? La trigonométrie (du grec τρίγωνος / trígonos, « triangulaire », et μέτρον / métron, « mesure ») est une branche des mathématiques qui traite des relations entre distances et angles dans les triangles et des fonctions trigonométriques telles que sinus, cosinus et tangente.
Article Wikipédia : trigonométrie.
Vous ne l'avez peut-être pas remarqué jusqu'à présent, mais les jeux vidéo sont remplis de triangles. Par exemple, imaginez un jeu vidéo avec des avions et que vous vouliez calculer la distance entre ces deux avions.

Vous avez x et y, les coordonnées cartésiennes de chaque avion, mais comment pouvez-vous calculer la longueur de cette ligne ? Eh bien, vous pouvez simplement tracer une ligne partant du centre de chaque avion, ce qui formera un triangle comme ceci.
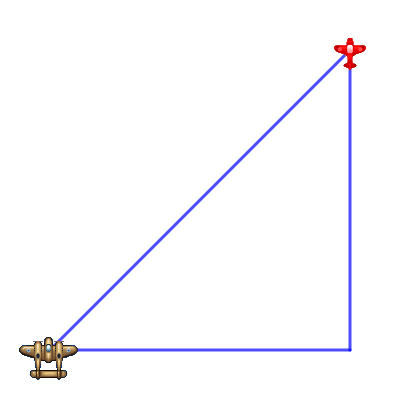
Puisque vous avez les coordonnées cartésiennes de chaque avion, avec x pour les abscisses et y pour les ordonnées, vous pouvez calculer la longueur de chacune des nouvelles lignes. Une fois que vous connaissez les longueurs des deux côtés du triangle, vous pouvez utiliser un peu de trigonométrie pour déterminer la longueur de la ligne diagonale, c'est-à-dire la distance entre ces deux avions.
Note :
Un des coins de ce triangle forme un angle droit de 90 degrés. Ce type de triangle est connu sous le nom de triangle rectangle, et c’est principalement avec ce genre de triangle que vous travaillerez tout au long de ce cours. Cependant, il existe d’autres types de triangles, comme les triangles équilatéraux, isocèles et quelconques. Pour ces triangles qui ne contiennent pas d’angle droit, on peut utiliser le théorème d'Al-Kashi. Ce mathématicien perse du XIVe siècle a généralisé le théorème de Pythagore pour les triangles non rectangles, permettant ainsi de calculer leurs différents angles et longueurs.
Article Vikidia : théorème d'Al-Kashi.
Article Wikipédia : théorème de Pythagore.
Article Vikidia : Al-Kashi.
Article Wikipédia : Pythagore.
Chaque fois que vous représentez des déplacements de sprite dans votre jeu vidéo sous forme de triangles avec un angle droit de 90 degrés, comme la relation spatiale entre les deux avions ci-dessus, vous pouvez utiliser les fonctions trigonométriques pour effectuer des calculs. En résumé, la trigonométrie est un outil précieux pour déterminer les longueurs des côtés de ces triangles et les angles entre eux. Pensez-y lorsque cela est possible : cela vous facilitera grandement la tâche.
Article Wikipédia : Sprite.
J'utiliserai plusieurs notations pour définir un angle, mais elles désignent toutes la même chose : alpha (α), bêta (β) et thêta (θ). Tout d'abord, nous allons aborder un peu de théorie. Pas d'inquiétude, je serai bref pour que vous puissiez comprendre rapidement. Voici les différentes parties qui composent un triangle rectangle :

Dans l'image ci-dessus, le côté oblique est appelé l’hypoténuse. Il se trouve toujours en face de l’angle de 90 degrés (également appelé angle droit) et est toujours le côté le plus long du triangle. Les deux autres côtés sont appelés le côté opposé et le côté adjacent. Dans cet exemple, un coin particulier du triangle, situé en bas à gauche, sert de référence.
Cependant, si vous regardez le triangle rectangle ci-dessous, les rôles des côtés opposé et adjacent sont inversés, tout comme la position du coin de référence, qui se trouve cette fois en haut à droite.

Alpha (α) et bêta (β) sont les noms des deux angles aigus d’un triangle rectangle. Vous pouvez les nommer comme vous le souhaitez, mais en général, alpha (α) est l'angle d'intérêt, tandis que bêta (β) est l'autre angle aigu complémentaire. Les côtés opposé et adjacent sont définis par rapport à l'angle alpha (α). Si vous connaissez un angle aigu (α ou β) et la longueur de l'un des côtés, les fonctions trigonométriques (sinus, cosinus et tangente) vous permettent de déterminer la longueur des autres côtés.

Vous pouvez utiliser une mnémotechnique très pratique pour vous rappeler les formules des fonctions trigonométriques de base : 'soh-cah-toa'. Cela correspond à :


Prenons un exemple : supposons que vous connaissez l'angle α entre les deux avions ci-dessus, qui est de 45°, ainsi que la longueur de l'hypoténuse, qui est de 10 u.l (unités de longueur). Vous pouvez ensuite substituer ces valeurs dans la formule :
sin(45) = opposé / hypoténuse
On remplace nos valeurs :
sin(45) = opposé / 10
Pour résoudre cette équation, nous appliquons les règles de calcul et effectuons un produit en croix.
Définition du produit en croix : si l'on a deux fractions égales alors le produit du numérateur de la première fraction par le dénominateur de la seconde est égale
au produit du numérateur de la seconde fraction par le dénominateur de la première. Cela peut être exprimé par l'équivalence suivante :
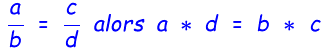
d'où :
opposé * 1 = sin(45) * 10
Si vous utilisez une calculatrice ou la boîtes noires de l'ordinateur, sin(45) vous renverra environ 0,707 (arrondi). Continuons :
opposé = 0.707 * 10
opposé = 7.07 u.l
Pensez aux fonctions sin, cos et tan comme des boîtes noires : vous leur fournissez un nombre en entrée, et elles vous renvoient un résultat. Ce sont des fonctions prédéfinies disponibles dans presque tous les langages de programmation. Nous examinerons cela de plus près dans l'éditeur de code de p5.js, en utilisant sa bibliothèque mathématique.
Les formules ci-dessus sont particulièrement utiles lorsque vous connaissez déjà un angle et une longueur d'un triangle rectangle. Cependant, ce n'est pas toujours le cas. Une autre approche consiste à exploiter les longueurs d'au moins deux côtés du triangle. Par exemple, si vous connaissez les longueurs de l'hypoténuse et d'un côté adjacent ou opposé, vous pouvez retrouver l'angle correspondant en utilisant les fonctions trigonométriques inverses, comme l'arcsinus, l'arccosinus ou l'arctangente. Pour ce faire, il suffit d'insérer ces valeurs dans la boîte noire mentionnée précédemment (c'est-à-dire un outil ou une calculatrice adaptée), qui calculera automatiquement l'angle à partir du rapport des longueurs. Cette méthode est particulièrement utile dans des situations où seuls les côtés du triangle sont mesurables, par exemple en géométrie pratique ou en topographie.


En d'autres termes :
Si sin (α) = β, alors arcsin (β) = α est également vrai.
Si cos (α) = β, alors arccos (β) = α est également vrai.
Si tan (α) = β, alors arctan (β) = α est également vrai.
La fonction sin est l'inverse de la fonction arcsin et vice-versa. De même, la fonction cos est l'inverse de la fonction arccos, et la fonction tan est
l'inverse de la fonction arctan. Parmi ces fonctions trigonométriques inverses, vous utiliserez le plus souvent arctan en pratique.
Sur les calculatrices, ces fonctions inverses sont généralement notées sin-1, cos-1, et tan-1 ou encore arcsin, arccos et arctan. Ce sont ces fonctions que nous utiliserons dans la boîte noire de notre éditeur de code p5.js. Ne vous inquiétez donc pas si vous les croisez.

Prenons un exemple avec notre deuxième mini-jeu vidéo, que nous allons programmer dans la rubrique « Algorithme », située dans la barre de menus. Supposons que vous connaissiez deux côtés d'un triangle rectangle représentant les trajectoires des deux avions ci-dessus : le côté opposé mesure 45 u.l (unités de longueur) et le côté adjacent mesure également 45 u.l.
Pour calculer l'angle α formé entre ces deux avions, nous allons utiliser la fonction de l'arc tangente (arctan), Cela se traduit en équation par :
α = arctan(opposé / adjacent)
On remplace nos valeurs :
α = arctan(45 / 45)
Si vous calculez l'arc tangent de 45/45 avec une calculatrice ou la boîte noire de votre ordinateur, vous obtiendrez un angle en degrés de
45° et en radians de PI/4 = 0.785 rad.
Dans notre mini-jeu vidéo, cet angle sera utilisé pour déterminer les trajectoires des balles tirées de l'avion ennemi vers l'avion mère à l'écran.
Voilà, ce sont toutes les formules de base que vous devez connaître ! Le choix de la formule à utiliser dépend des informations dont vous disposez. En général :
Nous avons exploré un aperçu des fonctions trigonométriques de base, mais la leçon théorique est loin d'être terminée. Il reste encore beaucoup à découvrir et à calculer avec les triangles.
Parfois, vous pouvez connaître la longueur de deux côtés d'un triangle et avoir besoin de déterminer la longueur du troisième côté, comme dans l'exemple au début de ce cours où nous devions calculer la distance entre les deux avions en haut de cette page web. C'est à ce moment-là que la trigonométrie et le théorème de Pythagore interviennent. Même si vous avez oublié tout le reste des mathématiques, il est probable que ce soit la seule formule dont vous vous souvenez :


Note : La fonction racine carrée est l'une des nombreuses fonctions mathématiques disponibles dans la bibliothèque mathématique de p5.js. Elle est pratiquement indispensable lorsque l'on programme avec notre boîte à outils mathématiques, notamment pour répondre à des besoins spécifiques, comme le calcul de l'hypoténuse d'un triangle rectangle, comme illustré ci-dessus.
Enfin, si vous connaissez la mesure de l'un des angles autres que l'angle droit dans un triangle rectangle, vous pouvez alors déterminer toutes les autres mesures des angles de ce triangle. En effet, dans un triangle rectangle, la somme des mesures de ses angles est toujours égale à 180 degrés. Vous savez déjà que l'un de ces angles est de 90 degrés :
α + β + 90° = 180°
Ou tout simplement :
α + β = 90°
α + β sont des angles complémentaires.
Les deux angles restants doivent être égale à 90 degrés. Donc, si vous savez l'angle α, vous savez aussi l'angle β, et vice-versa.
Propriété : La somme des mesures des angles, égale à 180°, est toujours vraie pour tous les triangles, qu'ils soient équilatéraux, isocèles, rectangles et quelconques, dans le cadre de la géométrie euclidienne des éléments d'Euclide.

Toutes ces définitions concernent la mesure d'un angle. Ainsi, un angle est défini comme suit :
Saillant si sa mesure est comprise entre 0° et 180°.
Plat si sa mesure vaut 180°.
Rentrant si sa mesure est comprise entre 180° et 360°.
Plein si sa mesure vaut 360°.
Aigu si sa mesure vaut entre 0° et 90°.
Obtus si sa mesure vaut entre 90° et 180°.
Droit si sa mesure vaut 90°.
Deux angles dont la somme des mesures est égale à 90° sont complémentaires.
Deux angles dont la somme des mesures est égale à 180° sont supplémentaires.
Par exemple, dans un triangle rectangle, les deux angles qui ne sont pas l'angle droit sont complémentaires.
Deux angles ayant le même sommet, un côté commun et situés de part et d'autre de ce côté est adjacent.


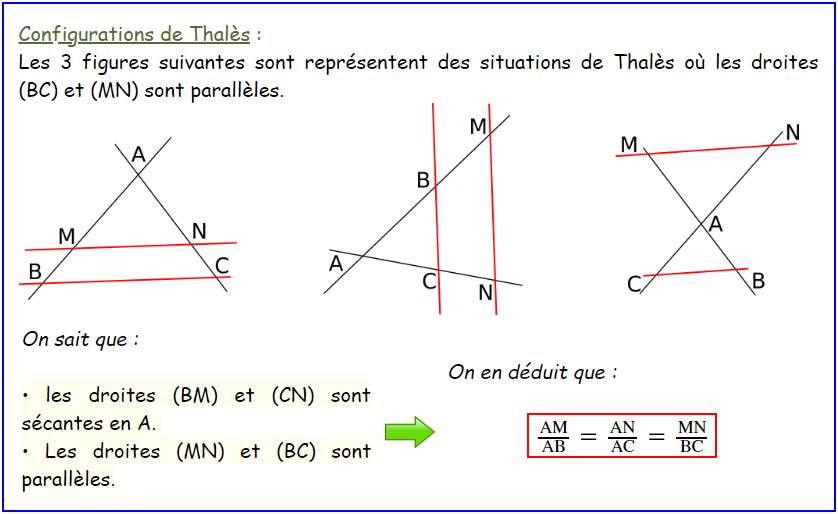

Vous n'aurez pas besoin du théorème de Thalès pour programmer nos mini-jeux vidéo sous la rubrique « Algorithme » située dans la barre de menus. J'ai inclus ce théorème de géométrie à titre de rappel des mathématiques en général, et plus particulièrement des notions de géométrie comme les angles et les mesures étudiés jusqu'ici. En revanche, dans notre mini-jeu vidéo, c'est la trigonométrie — avec l'arc tangent et les coordonnées polaires — qui sera pleinement mise à profit pour diriger les tirs de l'avion ennemi qui visent l'avion mère, capable de se déplacer librement sur l'écran.
Article Wikipédia : théorème de Thalès. Article Wikipédia : Thales de Milet. Article Wikipédia : théorème de géométrie.Voici les valeurs remarquables des angles les plus utilisés dans le cercle trigonométrique. Chaque colonne correspond à un angle, et chaque ligne indique sa mesure en degrés, en radians, ainsi que les valeurs de cos(x) et sin(x).
| 0° | 30° | 45° | 60° | 90° | 180° | |
|---|---|---|---|---|---|---|
| x en degrés | 0° | 30° | 45° | 60° | 90° | 180° |
| x en radians | 0 | π / 6 | π / 4 | π / 3 | π / 2 | π |
| cos(x) | 1 | √3 / 2 | √2 / 2 | 1 / 2 | 0 | -1 |
| sin(x) | 0 | 1 / 2 | √2 / 2 | √3 / 2 | 1 | 0 |
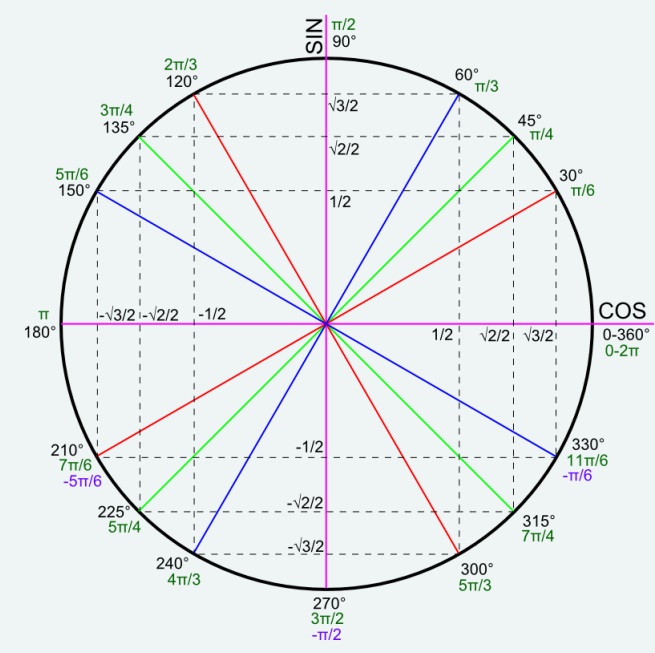
De ce tableau, et à l'aide du cercle trigonométrique ci-dessus, on déduit aisément les valeurs remarquables de sinus et cosinus pour
les angles entre 0 et 2π ou entre -π et 2π.
Note : Grâce au cercle trigonométrique, vous comprendrez, lorsque vous passerez à la rubrique
« Algorithme : Mini jeu vidéo sur l’analyse », comment effectuer la rotation de l’avion de notre mini-jeu vidéo selon la pente de sa
trajectoire, afin qu’il reste toujours aligné avec son mouvement parabolique.
Lorsque que nous avons besoin d'afficher une forme avec p5.js, il nous faut indiquer une position exprimée en pixels avec les coordonnées x et y. Ces coordonnées sont
appelées coordonnées cartésiennes, du nom de René Descartes, le mathématicien Français qui a développé ce que l'on appelle
l'espace cartésien au XVIIe siècle.
Un autre système de coordonnées utile est appelé coordonnées polaires décrit un point dans l'espace (en 2d : dans un plan)
comme un angle de rotation autour de l'origine et le rayon (la distance) depuis l'origine. Si on fait le parallèle avec les vecteurs : les coordonnées cartésiennes
sont les coordonnées {x, y} du vecteur. Les coordonnées polaires sont la norme (longueur) et la direction (angle) du vecteur, par contre, les fonctions de dessin
en p5.js ne savent pas utiliser les coordonnées polaires. Dès que nous voulons afficher quelque chose, nous devons indiquer les positions sous forme de coordonnées
cartésiennes {x, y}. Il est parfois pourtant beaucoup plus pratique de travailler avec les coordonnées polaires, lorsqu'on dessine. Heureusement pour nous,
grâce à la trigonométrie, nous pouvons convertir dans les deux sens entre le système polaire et le système cartésien. Cela nous permet de travailler avec le système
de coordonnées qui nous arrange mais toujours utiliser les coordonnées cartésiennes pour l'affichage.
Comme il s’agit d’un système bidimensionnel, chaque point est déterminé par les coordonnées polaires, qui sont la coordonnée radiale et la coordonnée angulaire.
La coordonnée radiale (souvent notée r ou ρ, et appelée rayon) exprime la distance du point à un point central appelé pôle (équivalent à l’origine des coordonnées
cartésiennes). La coordonnée angulaire (également appelée angle polaire ou azimut, et souvent notée t ou θ) exprime la mesure, dans le sens trigonométrique (sens positif),
de l’angle entre le point et la demi-droite d’angle 0°, appelée axe polaire (équivalente à l’axe des abscisses en coordonnées cartésiennes). Ce type de conversion
est très utile dans certains cas. Par exemple, déplacer une forme le long d'une trajectoire circulaire en utilisant les coordonnées cartésiennes n'est pas si
facile ! Alors, qu'au contraire, utiliser les coordonnées polaires, dans ce cas, est très simple : Il suffit simplement d'augmenter l'angle !




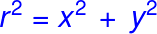

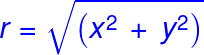

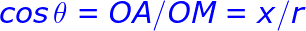

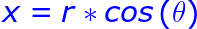


Ce cours sur la trigonométrie est maintenant terminé pour la théorie mais on va le reprendre côté code avec le langage de programmation JavaScript dans l'éditeur de code de p5.js pour programmer notre deuxième mini-jeu vidéo sous la rubrique « Algorithme » située dans la barre de menus.