Maintenant que nous savons calculer la dérivée d'une fonction carrée qui représente graphiquement une parabole, nous allons utiliser ces connaissances pour créer un mini-jeu vidéo où un avion se déplace sur une trajectoire parabolique sur l'écran. En utilisant les points de dérivée de la fonction carrée, nous pouvons ajuster la trajectoire de l'avion pour qu'elle suive la forme d'une parabole, ce qui rendra le mouvement de l'avion plus réaliste et captivant pour les joueurs.
Nous allons utiliser l'éditeur de code p5.js pour programmer nos algorithmes. Vous pouvez télécharger l'éditeur
ci-dessous et consulter les captures d'écran pour avoir une idée de son apparence. Si vous n'avez jamais programmé auparavant, vous pouvez cliquer sur le badge ci-dessous
pour accéder aux références de p5.js ou suivre ce lien : Introduction_p5js pour une introduction à la programmation avec
p5.js. Cela devrait vous permettre de comprendre les commandes de base de p5.js.
Si vous êtes déjà familiarisé avec un autre langage de programmation, vous devriez être en mesure de comprendre les algorithmes que je vais vous
présenter pour ce jeu vidéo.
p5.js
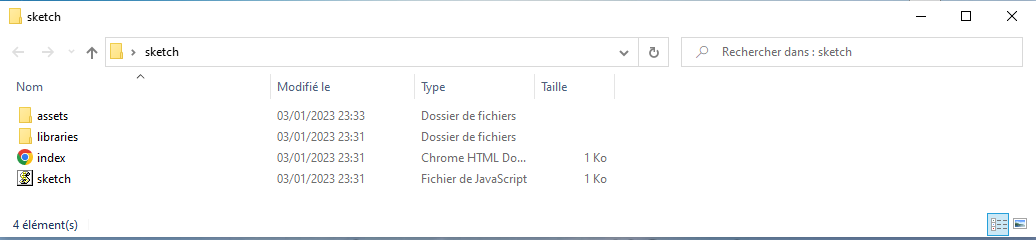
Les captures d'écran ci-dessus vous montrent la structure de votre projet, avec le fichier index.html qui contient les liens vers les différentes librairies de p5.js, ainsi que le fichier sketch.js qui est celui où vous écrirez le programme principal.
Je vous montrerai comment ajouter un script avec l'extension .js dans l'éditeur de code p5.js lorsque nous programmerons notre jeu vidéo final de type "shoot 'em up" à défilement vertical, sous la rubrique « Programmation » située dans la barre de menus. Pour l'instant, cela n'est pas nécessaire, car notre programme est court et tient sur un seul script nommé sketch.js. Vous pouvez sauvegarder votre projet sous un autre nom lorsque vous fermez l'éditeur de code p5.js.
/*******************************************
** Autheur de ce programme : unité1994
** tuto Analyse : calcul de dérivée
** Date le 24/10/2017
** Programmation JavaScript dans IDE P5.js
*******************************************/
// On définit toutes nos variables globales avant la méthode setup()
var x = -200, y = 0; coef_dir = -0.01;
// Fonction setup() appelée une seule fois au lancement du programme
function setup() {
// Taille de la fenêtre d'écran 600 par 800 pixels
createCanvas(600, 800);
// On charge nos images
img_avion = loadImage("assets/avion.png");
img_mer = loadImage("assets/fonds_mer.jpg");
}
// Function draw() lancer sans arrêt jusqu'à la fin du programme
function draw() {
// Affichage écran fonds mer
image(img_mer, 0, 0);
// Fonction mathématique y = -0.01 * x²
y = coef_dir * sq(x);
push();
translate(x + width/2, y + height/2);
// calcul de la dérivée : y = 0.01 * x² = 0.02 * x
// en paramètre de notre fonction de l'arc tangante (atan)
// dans le rotate
rotate(3 * PI/2 + atan(coef_dir * 2 * x));
// Affichage de l'image de l'avion aux coordonnées 0, 0 du translate
image(img_avion, 0, 0);
pop();
// mouvement de la trajectoire x = x + 2 sur l'abscisse des x sur la parabole
x += 2;
// On teste la sortie d'écran de l'avion
if(this.x > width/2) { this.x = -width/2; }
}
Ce code ci-dessus est un programme en utilisant la bibliothèque p5.js avec le langage JavaScript pour créer une animation qui affiche une image d'avion qui suit
une trajectoire en forme de parabole sur une image de fond d'océan. Il utilise plusieurs variables globales qui sont définies en haut du code avant la méthode setup() :
La méthode setup() est appelée une seule fois au début du programme et utilise la fonction createCanvas() pour créer une fenêtre d'affichage de
600 pixels de large par 800 pixels de haut. Elle charge également les images de l'avion et du fond d'océan en utilisant les fonctions loadImage().
La fonction draw() est ensuite appelée sans arrêt jusqu'à la fin du programme. Elle commence par afficher l'image de fond d'océan à l'aide de la fonction image().
Ensuite, elle utilise la formule mathématique y = coef_dir * x² pour calculer la position verticale de l'avion sur la parabole.
La fonction push() et
pop() est utilisée pour sauver et restaurer les transformations de la matrice de dessin. La fonction translate() est utilisée pour déplacer l'origine
de coordonnées de l'avion aux nouvelles coordonnées calculées. La fonction rotate() est utilisée pour faire tourner l'image de l'avion en fonction de la dérivée
de la parabole. Enfin, l'image de l'avion est affichée aux coordonnées 0, 0 du translate aux nouvelles coordonnées calculées.
Nous avons une fonction qui calcule la dérivée d'une courbe décrite par la fonction y = 0.01 * x² qui est égale à 0.02 * x. Cette dérivée est utilisée
pour faire une rotation dans un environnement graphique. La rotation est effectuée autour d'un angle donné par 3 * PI/2 + atan(coef_dir * 2 * x), où coef_dir
est un coefficient de direction. La fonction atan calcule l'arc tangente de coef_dir * 2 * x.
La variable x est ensuite incrémentée de 2 pour simuler le mouvement de l'avion le long de la parabole. Enfin, une condition de test est utilisée pour vérifier
si l'avion sort de l'écran à droite, et si c'est le cas, il est ramené à gauche de l'écran avec la valeur -width/2.
Avant de lancer notre mini-jeu vidéo ci-dessous, je vous donne les ressources graphiques dans un dossier assets à télécharger ci-dessous. Il faut prendre le dossier assets contenant les images et le placer dans le dossier de votre projet p5.js, sous la racine du dossier compressé. Vous pouvez voir les exemples de capture d'écran ci-dessous. Le dossier se nomme sketch et le dossier assets doit être placé à l'intérieur de ce dossier. Je vous rappelle que lorsque vous lancez p5.js, le nom du projet par défaut est sketch, mais vous pouvez lui donner un autre nom lors de la sauvegarde de votre projet.
assets
Maintenant, que vous avez le code source ci-dessus et votre dossier assets à l'intérieur du votre projet, copiez-le et collez-le dans l'éditeur de code de p5.js, puis lancez le programme en appuyant sur le bouton « flèche » en haut à gauche de votre éditeur de code. Vous pouvez tester et télécharger votre troisième mini-jeu vidéo ci-dessous.
Avion avec la dérivée
Une fois que vous aurez lancé votre programme avec la dérivée, vous verrez l'avion avec un mouvement réaliste sur sa trajectoire parabolique. Si vous voulez voir l'animation sans calculer sa dérivée, mettez des commentaires devant la fonction rotate(3 * PI/2 + atan(coef_dir * 2 * x)); en utilisant les deux barres obliques, comme ceci : // rotate(3 * PI/2 + atan(coef_dir * 2 * x));. Lorsque vous relancerez le programme, l'avion ne fera pas de rotation sur lui-même lorsqu'il suivra sa trajectoire parabolique, et son mouvement ne sera pas réaliste.
Mouvement de l'avion simplifié :
sans recours aux dérivées
Avion sans la dérivée
Je vais vous détailler le calcul de notre dérivée avec la capture d'écran ci-dessous et vous parler d'une anomalie sur notre parabole !
Nous avons tout d'abord assigné notre fonction carrée : y = -0.01 * x². Ensuite, nous avons calculé la dérivée de cette fonction, qui est égale à :y ' = -0.02 * x. Son nombre dérivé est égal à 4 pour x = -200, pour la première valeur. Cependant, l'avion est en mouvement permanent sur sa trajectoire parabolique, ce qui signifie qu'il existe plusieurs valeurs pour toute une série de dérivées qui évoluent par pas de 2 sur l'axe des abscisses (x).
Regardez le programme ci-dessus : nous avons x += 2, ce qui signifie, en langage de programmation informatique, x = x + 2. Il s'agit d'une affectation de variable, et non d'une équation mathématique, car les deux membres ne sont pas égaux. Autrement dit, nous ajoutons une valeur numérique entière à la variable x, qui s'incrémente de 2 à chaque étape.
Vous verrez l'axe de l'image de l'avion dans notre mini-jeu vidéo se caler sur la tangente à chaque point, et l'avion suivra ainsi sa trajectoire parabolique. Voilà ce qu'il faut savoir sur le calcul de la dérivée pour que le mouvement de l'avion soit réaliste.
Je rappelle qu'un polynôme ou un monome du second degré décrit une parabole, tournée vers le haut ou vers le bas, en fonction du signe de son coefficient directeur. Si le signe de ce coefficient est positif, la parabole sera tournée vers le haut ; si le signe de ce coefficient est négatif, la parabole sera tournée vers le bas.
Notre fonction y = -0.01 * x² a un coefficient directeur négatif, égal à coef_dir = -0.01. Mathématiquement, cette parabole devrait être tournée vers le bas. Pourtant, lorsqu'on lance le programme de notre mini-jeu vidéo, la parabole apparaît tournée vers le haut. Cette anomalie est liée à la conception des ordinateurs, qui ont été développés par les ingénieurs à partir de l'année 1973. Je vais vous expliquer plus en détail pourquoi cette anomalie se produit.
Si vous entrez cette fonction, y = -0.01 * x², dans des calculatrices graphiques ou d'autres logiciels mathématiques sur un PC, la parabole sera bien tournée vers le bas. Cependant, dans l'animation de notre programme de jeu sur PC, elle apparaît tournée vers le haut. Nous avons ici une anomalie mathématique.
Cette anomalie provient du repère orthonormé utilisé dans notre programme, ou plus précisément de l'axe d'origine (0, 0) qui se trouve en haut à gauche de notre fenêtre d'écran. En effet, dans ce repère, nous avons deux axes : l'axe des abscisses (x), qui est horizontal, et l'axe des ordonnées (y), qui est vertical. L'anomalie réside dans le fait que l'axe des ordonnées (y), situé sur la verticale, est inversé dans notre repère orthonormé.
C'est pour cette raison que notre parabole est tournée vers le haut et non vers le bas. Cette inversion des axes peut aussi causer des aberrations dans d'autres calculs mathématiques, comme la trigonométrie sur PC avec sortie graphique. Par exemple, lorsque l'on mesure un angle, au lieu de suivre le sens positif, contraire aux aiguilles d'une montre, l'angle sera mesuré dans le sens inverse. Cela est dû à la convention héritée des premiers micro-ordinateurs, conçus à partir de 1973, qui utilisaient des écrans à balayage.
L'affichage à balayage : dans le cas des téléviseurs et des écrans d’ordinateurs, toute la face du tube est parcourue
selon un trajet bien défini, et l’image est créée en faisant varier l’intensité du flux d’électrons (le faisceau), et donc l’intensité lumineuse du spot, au long
de son parcours. Le flux dans tous les téléviseurs modernes est dévié par un champ magnétique appliqué sur le col du tube par un « joug magnétique »
(magnetic yoke en anglais), qui est composé de bobines (souvent deux) enroulées sur du ferrite et contrôlées par un circuit électronique. C’est
un balayage par déflexion magnétique.
Au cours du balayage, le faisceau parcourt de gauche à droite des lignes qui se succèdent de haut en bas (comme les lignes d’un livre), le retour à la
ligne suivante et en début de page se fait à faisceau éteint.
Testez cette fonction, y = -0.01 * x², sur l'émulateur de la NumWorks, et vous verrez que la parabole sera ouverte vers le bas, comme cela :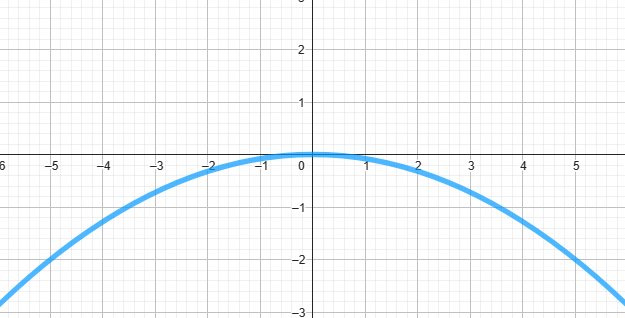 
. Cependant, dans notre programme de jeu vidéo, elle apparaît tournée vers le haut, comme cela : 
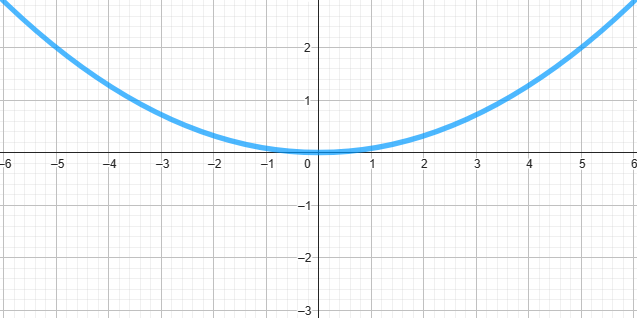. Comme je l'ai mentionné précédemment, l'axe des ordonnées (y), qui est sur la verticale, est inversé sur les écrans des ordinateurs. Cela est dû à la conception des ordinateurs par les ingénieurs depuis 1973.
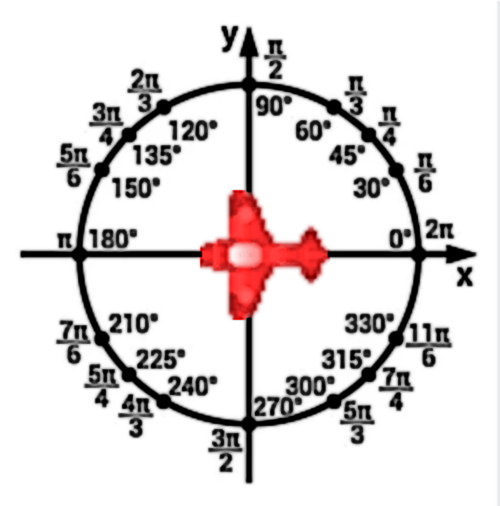
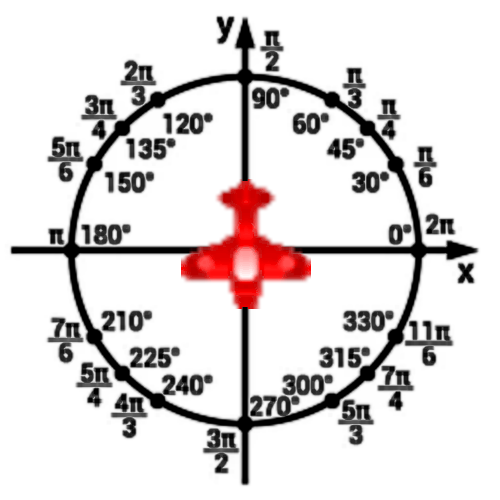
Je voulais préciser un détail concernant le calcul de notre dérivée dans le programme ci-dessus. Le calcul se fait dans la fonction rotate(), et plus précisément dans la fonction atan(), comme ceci : rotate(3 * PI/2 + atan(coef_dir * 2 * x));. Vous voyez le terme 3 * PI/2 : l'avion est bien positionné sur le bon angle par rapport à l'image elle-même. Autrement dit, la queue de l'avion pointe vers le haut de notre fenêtre d'écran, tandis que le cockpit pointe vers le bas. Cela correspond à ce que l'on observe sur notre cercle trigonométrique de droite ci-dessus, où le cockpit de l'avion est orienté vers 3 * PI/2.
Si vous changez la valeur de 3 * PI/2 par une autre valeur, comme PI par exemple, l'avion pointera vers la gauche, comme on peut le voir sur le cercle trigonométrique de gauche ci-dessus, avant le départ de son mouvement parabolique.
Ensuite, l'avion suivra la pente de la tangente, car nous additionnons un angle en RADIANS au calcul de la dérivée, comme ceci : 3 * PI/2 + atan(coef_dir * 2 * x), qui est dans la fonction atan(). Cette fonction renvoie l'arc de la tangente d'une valeur. Elle attend des valeurs dans la plage de -Infinity à Infinity (exclusif), et renvoie des résultats dans la plage de -PI/2 à PI/2 si angleMode est en RADIANS, ou de -90 à 90 si angleMode est en DEGREES. Essayez de changer des valeurs sur le cercle trigonométrique entre -PI/2 et PI/2 et vous verrez par vous-même les effets.
Une dernière précision : l'image de l'avion dans notre dossier assets est positionnée comme mentionné plus haut. La queue de l'avion pointe vers le haut de notre fenêtre d'écran, tandis que le cockpit pointe vers le bas, comme illustré ci-contre : 
Si vous prenez l'image dans le dossier assets et que vous la transformez en miroir vertical avec un logiciel d'infographie tel que Photoshop
ou GIMP, comme illustré ci-contre : 
, l'image de l'avion pointera comme prévu lorsque vous lancerez le programme. Cela s'explique par l'angle 3 * PI/2 dans la fonction rotate(3 * PI/2 + atan(coef_dir * 2 * x)).
La queue de l'avion pointera vers le bas avant le départ de sa trajectoire, comme montré sur les cercles trigonométriques ci-dessus. Vous devriez comprendre le lien. Sinon, vous pouvez simplement garder la bonne image dans le dossier assets et dans la fonction atan(), qui est additionnée à l'angle en RADIANS, mettez PI/2 au lieu de 3 * PI/2. Vous obtiendrez alors le même résultat que si vous aviez transformé l'image en miroir vertical dans votre logiciel d'infographie.
Voilà, nous avons terminé les algorithmes de ce troisième et dernier mini-jeu vidéo avec nos calculs de dérivées. Vous pouvez maintenant passer à la suite dans la rubrique « Programmation » située dans la barre de menus pour développer notre shoot 'em up à défilement vertical.
