Dans ce cours, vous apprendrez à calculer les dérivées des fonctions carrées et affines. Nous développerons également un mini-jeu vidéo où un avion suivra une trajectoire parabolique sur l'écran de votre PC.
Ce troisième mini-jeu vidéo nécessitera de calculer la dérivée d'une fonction carrée afin de simuler un mouvement réaliste de l'avion lors de sa trajectoire parabolique. La dérivée sera utilisée à l'intérieur de la fonction atan(), qui renvoie l'arc tangente d'une valeur comprise entre -π/2 et π/2 lorsque angleMode est réglé sur RADIANS, ou entre -90° et 90° lorsqu'il est réglé sur DEGREES. Nous détaillerons ces calculs dans la rubrique « Algorithme » située dans la barre de menus.
En mathématiques, la dérivée d'une fonction d'une variable réelle mesure l'ampleur du changement de la valeur de la fonction (valeur de sortie) par rapport à un petit
changement de son argument (valeur d'entrée). Les calculs de dérivées sont un outil fondamental du calcul infinitésimal. Par exemple, la dérivée de la position d'un
objet en mouvement par rapport au temps est la vitesse (instantanée) de l'objet.
La dérivée est très importante car on s’en sert tout le temps dans les études de fonction. L’avantage c’est qu’il n’y a pratiquement que des formules à apprendre, et une
fois que vous les connaissez, c’est extrêmement simple !
Quand on a une fonction ƒ, on peut calculer une autre fonction que l’on note ƒ ‘ (à prononcer ƒ prime), et qu’on appelle la dérivée. Nous verrons plus tard l’utilité de
ƒ ‘. L’objectif est tout d’abord de savoir comment calculer cette dérivée ƒ ‘ à partir de la fonction ƒ. Pour cela c’est très simple : on apprend les formules !

Note : Dans ce cours, nous utiliserons la notation ƒ '(x) pour désigner la dérivée d'une fonction ƒ(x). Cependant, lors de la programmation de notre troisième mini-jeu vidéo, sous la rubrique « Algorithme » de la barre de menus, nous adopterons la notation y ' pour représenter la dérivée de la fonction y. Dans le programme, cela revient au même, la seule différence réside dans la définition des fonctions. Si la liste des calculs de dérivées ci-dessus vous semble difficile à comprendre, ne vous inquiétez pas. Continuez la lecture : vous apprendrez à calculer la dérivée d'une fonction carrée ainsi que celle d'une fonction affine.
Note : La fonction carrée, souvent notée ƒ(x) = x2, est un exemple particulier de fonction quadratique. Une fonction quadratique est une fonction polynomiale de degré 2, généralement exprimée sous la forme ƒ(x) = ax2 + bx + c, où a, b et c sont des coefficients constant et a ≠ 0. Dans le cas de la fonction carrée, les coefficients b et c sont égaux à zéro, ce qui simplifie l'expression à ƒ(x) = x2.
Les fonctions quadratiques, y compris la fonction carrée, produisent des graphes en forme de parabole. Ces paraboles peuvent être orientées vers le haut ou vers le bas selon le signe du coefficient a, et elles sont symétriques par rapport à un axe vertical appelé axe de symétrie.
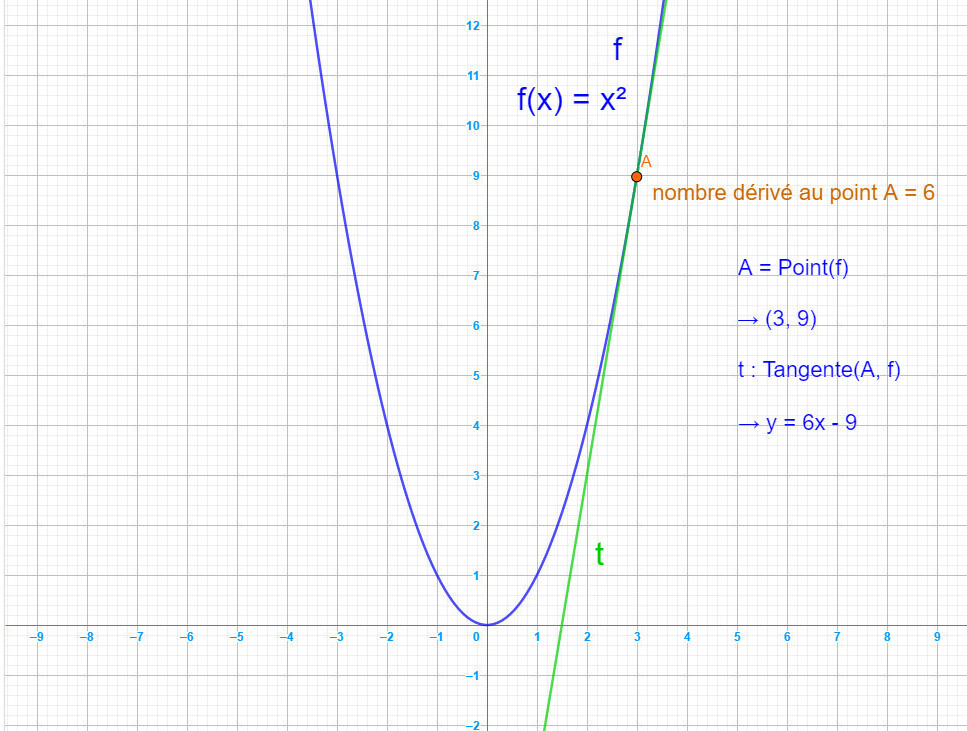
Dans l'image ci-dessous, nous observons graphiquement le nombre dérivé au point A de la tangente t à la courbe 𝑓. Nous avons choisi une courbe représentant la fonction carrée x2, qui est un polynôme du second degré et une fonction parabolique. Cette fonction, une parabole tournée vers le haut en raison du signe positif de son coefficient principal, est symétrique par rapport à l'axe des ordonnées dans un repère orthogonal.
Que remarque-t-on ? Le nombre dérivé au point A est égale à -6. Cela signifie que la pente de la tangente t à la courbe 𝑓 en ce point a un coefficient directeur de -6.

Dans l'image ci-dessous, le nombre dérivé au point A est égal à 0. Cela signifie que le coefficient directeur de la pente de la tangente t à la courbe 𝑓 est nul.

Dans l'image ci-dessous, le nombre dérivé en A est égal à 6. Cela signifie que la tangente t, tracée à la courbe 𝑓 en ce point, a une pente dont le coefficient directeur est de 6.
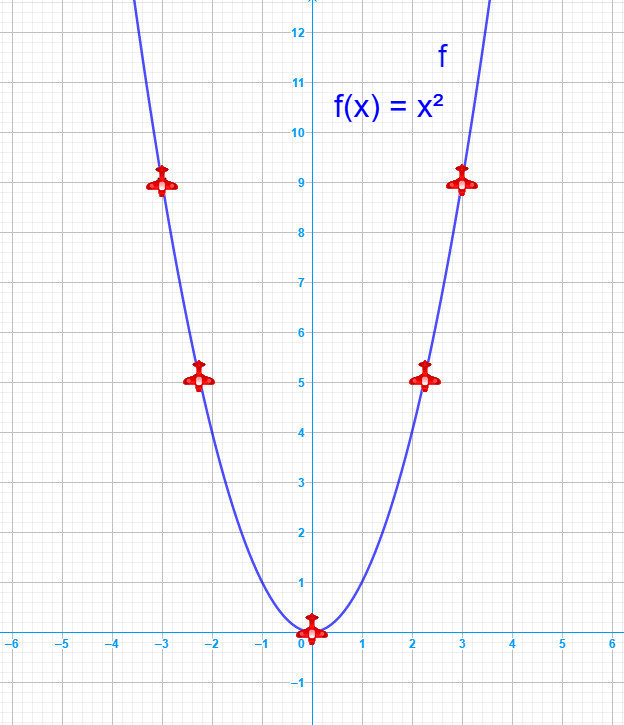
Note : Avez-vous une idée de pourquoi nous aurons besoin de calculer la dérivée de la fonction carrée dans notre troisième mini-jeu vidéo ? Laissez-moi vous expliquer. La dérivée de la fonction carrée est essentielle pour créer un mouvement réaliste de l'avion. En utilisant les points de dérivée, nous pouvons ajuster l'orientation de l'image de l'avion afin qu'il suive la tangente des courbes de la trajectoire parabolique. Cela permet à l'avion de faire une rotation sur lui-même. Sans ces calculs, l'avion ne pourrait pas effectuer cette rotation. Les images ci-dessous illustreront ce concept plus clairement.
Ici, l'avion effectue une rotation sur lui-même le long de sa trajectoire parabolique, car nous calculons les dérivées, c'est-à-dire les coefficients directeurs des tangentes à la fonction carrée représentant la courbe 𝑓.

Ici, l'avion ne tourne pas sur lui-même le long de sa trajectoire parabolique, car nous ne calculons pas les dérivées de la fonction carrée représentant la courbe 𝑓.

Pour calculer la dérivée de la fonction carrée, on se réfère au tableau des dérivées ci-dessous. On constate que la dérivée de x2, est égale à 2x.
C'est tout ce dont on a besoin pour programmer notre troisième mini-jeu vidéo pour le moment. Cependant, je vais vous vous expliquer, pas à pas, ci-dessous comment calculer la dérivée d'une fonction carrée et d'une fonction affine.

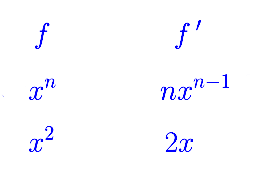
pour calculer la dériver de x2 en utilisant la formule générale ƒ '(x2) = n · xn-1 :
Maintenant, que vous savez calculer la dériver d'une fonction carrée, on va voir deux exemples ci-dessous, on va calculer la dériver de deux fonctions carrées avec un
coefficient directeur égal à 3.5 et un coefficient directeur égal à 5 :


Nous allons maintenant calculer la dérivée de deux fonctions carrées en utilisant les variables symboliques présentées ci-dessous :


La fonction carrée est un cas particulier des fonctions du second degré. Elle se distingue par l'absence de décalage ou de transformation : son expression est simplement ƒ(x) = x2.
Une fonction du second degré est une fonction mathématique qui s'exprime sous la forme générale :
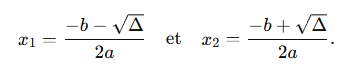
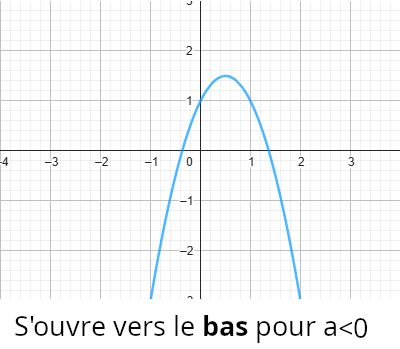
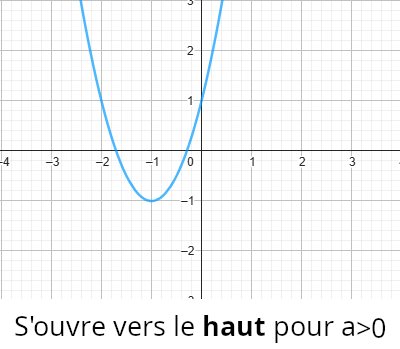
Le graphique d’une fonction du second degré est appelé une parabole en référence à sa forme. L’orientation de la parabole dépend du signe du coefficient a dans ƒ(x) = ax2 + bx + c; elle s’ouvre vers le haut si le coefficient directeur est positif et vers le bas s’il est négatif.
Définition d'une fonction affine
On appelle fonction affine toute fonction ƒ dont l'expression peut s'écrire sous la forme ƒ(x) = ax + b où a et b sont des constantes. Ce nombre a est appellé
coefficient directeur de la fonction affine ƒ. Ce nombre b est appelé ordonnée à l'origine de la fonction affine ƒ.
La représentation graphique d'une fonction affine est une droite non parallèle à l'axe des ordonnées, sauf si a = 0 auquel cas la fonction est constante.

Note : Dans notre jeu de type shoot 'em up à défilement vertical que l'on va programmer ensemble sous la rubrique « Programmation » située dans la barre de menus, nous utiliserons des dérivées de fonctions carrées avec un coefficient directeur négatif, ainsi que des fonctions affines avec un coefficient directeur positives et négatives, et des fonctions constantes, pour la programmation dans l'éditeur de code de p5.js.
Je vais vous montrer comment calculer la dérivée d'une fonction affine. Le calcul de la dérivée d'une fonction affine diffère de celui d'une fonction carrée, mais il est très simple. Regardez le tableau des dérivées ci-dessus :
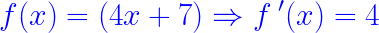
Commençons par dériver 4x. On dérive x, ce qui nous donne 1 d'après le tableau des dérivées ci-dessus. Ensuite, on multiplie par 4, le coefficient qui est devant x. Cela donne 4 * 1 = 4.
Ensuite, on dérive 7. Puisque 7 est une constante, sa dérivée est 0 (je vous rappelle que la dérivée d'une constante est toujours 0).
Ainsi, la dérivée de la fonction ƒ(x) = (4x + 7) est : ƒ '(x) = 4.
Voici un autre exemple : nous allons dériver une fonction affine ayant un coefficient directeur égal à -11 et une ordonnée à l'origine égale à 5. La fonction est définie comme suit :
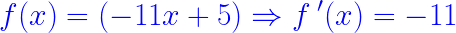
Commençons par dériver -11x. On dérive x, ce qui nous donne 1 d'après le tableau des dérivées ci-dessus. Ensuite, on multiplie par -11, le coefficient qui est devant x. Cela donne -11 * 1 = -11.
Ensuite, on dérive 5. Puisque 5 est une constante, sa dérivée est 0 (je vous rappelle que la dérivée d'une constante est toujours 0).
Ainsi, la dérivée de la fonction ƒ(x) = (-11x + 5) est : ƒ '(x) = -11.
Nous allons maintenant calculer la dérivée d'une fonction affine en utilisant les variables symboliques présentées ci-dessous :
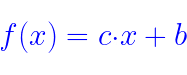
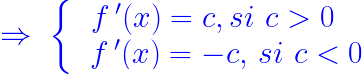
Le résultat de ƒ '(x) sera une constante positive ou négative, égale au coefficient directeur devant la variable x. Cette constante est positive si le coefficient directeur est positif, et négative si celui-ci est négatif. Rien de plus simple !
D'une pierre deux coups ! En sachant calculer la dérivée d'une fonction carrée et d'une fonction affine, vous pouvez désormais calculer la dérivée de n'importe quel polynôme, quel que soit son degré, pourvu qu'il soit de cette forme :
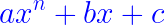
où a, b et c ∈ ℝ avec a ≠ 0
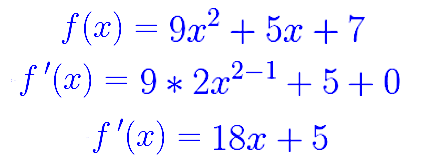
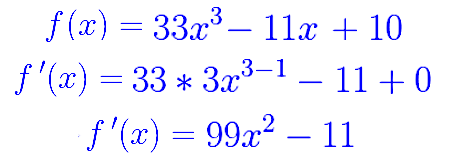
Si vous souhaitez en savoir plus sur les dérivées, voici une application que j'ai développée en 2016 : Maths trajectoires. Cette application explore les pentes des tangentes de différentes trajectoires, telles que :
Dans cette application, vous découvrirez des mouvements réalistes d'avions au-dessus d'un décor océanique. Vous pourrez également interagir avec des commandes à curseurs sur un décor désertique. En modifiant les paramètres, vous ajusterez en temps réel les pentes des tangentes, les trajectoires des avions, ainsi que leur nombre total.
Ce cours sur l'analyse est maintenant terminé pour la théorie mais on va le reprendre côté code avec le langage de programmation JavaScript dans l'éditeur de code de p5.js pour programmer notre troisième mini-jeu vidéo sous la rubrique « Algorithme » située dans la barre de menus.