Mini-jeu sur la trigonométrie

Maintenant que nous avons compris les concepts fondamentaux de la trigonométrie, nous allons mettre en pratique ces connaissances pour développer un programme de mini-jeu vidéo où un avion ennemi se déplace de haut en bas à travers l'écran et tire des balles en visant un avion mère qui pourra également se déplacer sur l'écran. La trigonométrie nous permet de calculer les relations entre les distances et les angles 𝜃 dans les triangles rectangles avec des fonctions trigonométriques telles que le sinus (sin), le cosinus (cos), la tangente (tan), ainsi que leurs fonctions inverses : l'arcsinus (arcsin), l'arccosinus (arccos) et l'arctangente (arctan). Ce qui est nécessaire pour retrouver les différents angles 𝜃 d'où seront tirer les balles de l'avion ennemi visant l'avion mère.

Il est possible d'utiliser un vecteur (PVector) pour les mouvements de l'avion mère et de simples variables x et y pour le mouvement de l'avion ennemi visant l'avion mère. Ensuite, on peut utiliser l'arc tangente pour calculer l'angle 𝜃 entre les deux avions, comme on l'a vu dans les calculs de distance et d'angle avec les triangles rectangles sous la rubrique « Trigonométrie » précédemment. Enfin, on peut utiliser des calculs de coordonnées polaires pour diriger les balles de l'avion ennemi visant l'avion mère.

Nous allons utiliser l'éditeur de code p5.js pour programmer nos algorithmes. Vous pouvez télécharger l'éditeur ci-dessous et consulter les captures d'écran pour avoir une idée de son apparence. Si vous n'avez jamais programmé auparavant, vous pouvez cliquer sur le badge ci-dessous pour accéder aux références de p5.js ou suivre ce lien : Introduction_p5js pour une introduction à la programmation avec p5.js. Cela devrait vous permettre de comprendre les commandes de base de p5.js. Si vous êtes déjà familiarisé avec un autre langage de programmation, vous devriez être en mesure de comprendre les algorithmes que je vais vous présenter pour ce jeu vidéo.

p5.js

Les captures d'écran ci-dessus vous montrent la structure de votre projet, avec le fichier index.html qui contient les liens vers les différentes librairies de p5.js, ainsi que le fichier sketch.js qui est celui où vous écrirez le programme principal.

Je vous montrerai comment ajouter un script avec l'extension .js dans l'éditeur de code p5.js lorsque nous programmerons notre jeu vidéo final de type shoot 'em up à défilement vertical, sous la rubrique « Programmation » située dans la barre de menus. Pour l'instant, cela n'est pas nécessaire, car notre programme est court et tient sur un seul script nommé sketch.js. Vous pouvez sauvegarder votre projet sous un autre nom lorsque vous fermez l'éditeur de code p5.js.

Examen des algorithmes clés utilisés dans notre jeu vidéo

Voici les algorithmes de base pour programmer notre mini-jeu vidéo. Les commentaires du programme expliquent les principales commandes exécutées par p5.js.

/**************************************************************  
    Autheur de ce programme : unité1994                      
    Date le 11/11/2017 - Avion atan(arctan)                   
    Programmation JavaScript dans IDE P5.js                                   

 ****************************************************************/

//  On définit toutes nos variables globales avant la fonction setup()                                                                                                                
//  Vitesse de l'avion
var speed_Aircraft; 

//  5 booleans qui prennent la valeur soit (true) ou (false) vrai où faut
//  pour touche clavière appuyée ou relâchée
var ri, le, up, dw;   

//  Variables pour tir de munitions
//  Coordonnées cartésiennes avion ennemi
//  Coordonnées polaires mouvement munitions de l'avion ennemi
var x_tireur, y_tireur, x_cible, y_cible, theta, r = 0, vitesse;   
var x_bullet, y_bullet; 
var x_enemy = 0; y_enemy = 0;
//  Variable booléenne on = true
var on = true;


//  Fonction setup() appelée une seule fois au lancement du programme
function setup() {
  //  Taille de la fenêtre d'écran 600 par 800 pixels
  createCanvas(600, 800);

  //  PVector v1 pour coordonnées cartésiennes v1.x et v1.y de l'avion (vecteur 2d)
  v1 = createVector(width/2,  height/2 + 300);

  //  On charge nos images
  img_avion_mere      = loadImage("assets/avion_mere.png");
  img_mer             = loadImage("assets/fonds_mer.jpg");
  img_enemy           = loadImage("assets/avion.png");
  img_balle           = loadImage("assets/balle_fire.png");
  speed_Aircraft      = 3;  //  Vitesse avion mère
  x_enemy             = width/2;
}

//  Fonction draw() appelée sans arrêt jusqu'à la fin du programme
function draw() {

  // Affichage écran fonds mer
  image(img_mer, 0, 0);
  
  //  Centre le repère d'ancrage sur l'image
  imageMode(CENTER);
  //  Affiche l'image de l'avion ennemi aux coordonnées cartésiennes x_enemy, y_enemy
  image(img_enemy, x_enemy, y_enemy);
  //  Remets le mode imageMode par défaut
  //  le repère d'ancrage sur l'image est en haut à gauche
  imageMode(CORNER);
 
  //  Évolution de l'avion ennemi plus test de sortie d'écran
  //  L'avion ennemi se déplace sur l'ordonnée y_enemy par pas de 2 pixels vers le bas
  y_enemy += 2;
   //  Teste la sortie d'ecran de l'avion ennemi
  if(y_enemy > 850) y_enemy = -50;

  //  Appel de la fonction action_Aircraft()
  action_Aircraft();
  //  Appel de la fonction action_Enemy()
  action_Enemy();
  
  //  Centre le repère de l'ancrage sur l'image
  imageMode(CENTER);
  //  Affichage de l'image de l'avion aux coordonnées v1.x, v1.y
  image(img_avion_mere, v1.x, v1.y);
  textSize(18);
  //  Remets le mode imagetMode par défaut
  //  le repère d'ancrage sur l'image est en haut à gauche
  imageMode(CORNER);
  
  //  Affichage sur la fenêtre d'écran du vecteur v1 
  //  avec ses coordonnées catésiennes v1.x et v1.y en temps réel
  fill(255);  //  Couleur blanc
  text("PVector (avion mère) : " + "v1.x = " + v1.x + " v1.y = " + v1.y, 10, 25);
}

//  Fonction keyPressed()
//  Évènemment si on presse sur une touche sur le clavier
function keyPressed() {
  //  On teste la touche flèche droite si elle est appuyée
  if (keyCode == RIGHT_ARROW) {
    ri = true;
  } else
  //  On teste la touche flèche gauche si elle est appuyée
  if (keyCode == LEFT_ARROW) {
    le = true;
  } else
  //  On teste la touche flèche basse si elle est appuyée
  if (keyCode == DOWN_ARROW) {
    dw = true;
  }
  //  On teste la touche flèche haute si elle est appuyée
  if (keyCode == UP_ARROW) {
    up = true;
  }
}

//  Fonction keyReleased()
//  Évènemment si on relâche une touche du clavier 
function keyReleased() {
  //  On teste la touche flèche droite si elle est relâchée
  if (keyCode == RIGHT_ARROW) {
    ri = false;
  }
  //  On teste la touche flèche gauche si elle est relâchée
  else if (keyCode == LEFT_ARROW) {
    le = false;
  }
  //  On teste la touche flèche basse si elle est relâchée
  else if (keyCode == DOWN_ARROW) {
    dw = false;
  }
  //  On teste la touche flèche haute si elle est relâchée
  if (keyCode == UP_ARROW) {
    up = false;
  }

}

//  Fonction Action_Aircraft()  
function action_Aircraft() {
  //  On teste la touche flèche droite si elle est appuyée 
  if (ri === true) {
    //  L'avion se déplace à droite de l'écran
    v1.x = v1.x + speed_Aircraft;
    //  On teste la sortie de l'avion à droite de l'écran
    if (v1.x > width - 30) v1.x = width - 30;
  }
  //  On teste la touche flèche gauche si elle est appuyée 
  if (le === true) {
    //  L'avion se déplace à gauche de l'écran
    v1.x = v1.x - speed_Aircraft;
    //  On teste la sortie d'écran de l'avion à gauche  
    if (v1.x < 30) v1.x = 30;
  }
  //  On teste la touche fléche basse si elle est appuyée 
  if (dw === true) {
    //  L'avion se déplace en bas de l'écran 
    v1.y = v1.y + speed_Aircraft;
    //  On teste la sortie de l'avion en bas de l'écran
    if (v1.y > height - 22) v1.y = height - 22;
  }
  //  On teste la touche fléche haute si elle est appuyée 
  if (up === true) {
    //  L'avion se déplace en haut de l'écran   
    v1.y = v1.y - speed_Aircraft;
    //  On teste la sortie de l'avion en haut de l'écran
    if (v1.y < 22) v1.y = 22;
  }
}

//  Fonction action_Enemy()  
function action_Enemy() {
  
  //  On rentre dans notre condition car la variable booléenne
  //  on = true on affecte plusieurs variables à la suite,
  //  sinon les calculs  
  //  de l'arc tangente et polaires ne peuvent pas se faire,
  //  on copie les coordonnées cartésiennes de l'avion ennemi,
  //  ici x_enemy et y_enemy aux variables x_tireur et y_tireur,
  //  on copie les coordonnées cartésiennes de l'avion mére,
  //  avec notre vecteur v1.x et v1.y aux variables x_cible et y_cible,
  //  cela nous servira quand on fera le calcul de l'arc tangent,
  //  pour retrouver l'angle entre l'avion mère et l'avion ennemi,
  //  cela nous servira pour le calcul des coordonnées polaires, 
  //  avec r pour le rayon qui évolue et qui dirigera les balles,
  //  de l'avion ennemi en visant l'avion mére,
  //  une fois affecter les variables, on ressort de la condition,
  //  avec on = false;
  if(on) {
    x_tireur         = x_enemy;
    y_tireur         = y_enemy;   
    x_cible          = v1.x;
    y_cible          = v1.y; 
    r = 0;
    on = false;
   }
   
   if ( r===0 ) {
    if (x_cible >= x_tireur) {
      //  On calcule l'angle de tir avec l'arc tangent
      theta = atan((y_cible-y_tireur) / (x_cible-x_tireur));  
      //  On affecte une valeur positive tirée au hasard entre 2 et 5 à la variable vitesse
      vitesse = random(2, 5);
    } else
    {
      //  On calcule l'angle de tir avec l'arc tangent
      theta = atan((y_cible-y_tireur) / (x_cible-x_tireur));  
      //  On affecte une valeur négative tirée au hasard entre -2 et -5 à la variable vitesse
      vitesse  = -(random(2,5));
    }
  }
  
  //  Calcul des coordonnées polaires des balles de l'avion ennemi
  r += vitesse;
  x_bullet = cos(theta) * r + x_tireur;
  y_bullet = sin(theta) * r + y_tireur;
  
  //  On teste les sorties d'écran
  //  des coordonnées polaires x_bullet et y_bullet (balles de l'avion ennemi)
  if(x_bullet > width || x_bullet < 0 || y_bullet > height || y_bullet < 0) {
    on = true;
  }
  
  //  Affichage des balles de l'avion ennemi
  imageMode(CENTER);
  image(img_balle, x_bullet, y_bullet); 
  imageMode(CORNER);
}

Analyse détaillée des algorithmes du programme

Ce code ci-dessus est un programme en utilisant la bibliothèque p5.js avec le langage JavaScript pour créer une animation de type shooter dans un navigateur web. Il utilise des images pour afficher les différents éléments de jeu (avion mère, avion ennemi, fond d'écran de mer, etc.) et des variables pour stocker les différentes informations nécessaires au fonctionnement du jeu.

Les variables globales déclarées en haut du code incluent :

• speed_Aircraft qui stocke la vitesse de l'avion mère
• 4 variables booléennes (ri, le, up, dw) qui enregistrent si une touche de direction est enfoncée ou relâchée
• Variables pour le tir de munitions, y compris les coordonnées cartésiennes de l'avion ennemi, les coordonnées polaires de mouvement des munitions de l'avion ennemi et une variable booléenne on qui est utilisée pour déterminer si l'avion ennemi est en train de tirer.

• x_tireur : la coordonnée x de l'avion ennemi qui tire
• y_tireur : la coordonnée y de l'avion ennemi qui tire
• x_cible : la coordonnée x de la cible (l'avion mère)
• y_cible : la coordonnée y de la cible (l'avion mère)
• r : représente le rayon dans un système de coordonnées polaires qui dirigera les balles de l'avion ennemi pour viser l'avion mère. La valeur de "r" est initialement définie comme 0 et est ensuite incrémentée à chaque itération de la fonction par la vitesse choisie au hasard entre 2 et 5 ou entre -2 et -5.
• on : un booléen qui indique si le tir est actif ou non
• theta : l'angle de tir (calculé avec atan)
• vitesse : la vitesse de la balle
• x_bullet : la coordonnée x de la balle
• y_bullet : la coordonnée y de la balle
• img_balle : une image de la balle

1. Si la variable on est true, c'est-à-dire vraie, alors les coordonnées de l'avion ennemi qui tire (x_tireur et y_tireur) sont mises à jour pour correspondre à celles de l'avion ennemi et les coordonnées de la cible, notre avion mère (x_cible et y_cible) sont mises à jour pour correspondre à celles du joueur. La variable "r" est remise à zéro et la variable on est remise à false, (faux).
   
   
2. Si r est égal à zéro, alors l'angle de tir (theta) est calculé en utilisant l'arc tangente entre la cible, notre avion mère et l'avion ennemi qui tire. Ensuite, une vitesse positive ou négative est tirée au hasard entre 2 et 5 et affectée à la variable vitesse.
   
   
3. Les coordonnées polaires de la balle sont calculées en utilisant les valeurs de theta, r, x_tireur et y_tireur.
   
   
4. Les coordonnées de la balle sont testées pour voir si elles sortent de l'écran. Si c'est le cas, la variable on est remise à true, c'est-à-dire vraie.
   
   
5. Enfin, l'image de la balle est affichée à ses coordonnées calculées.

Avant de lancer notre mini-jeu vidéo ci-dessous, je vous donne les ressources graphiques dans un dossier assets à télécharger ci-dessous. Il faut prendre le dossier assets contenant les images et le placer dans le dossier de votre projet p5.js, sous la racine du dossier compressé. Vous pouvez voir les exemples de capture d'écran ci-dessous. Le dossier se nomme sketch et le dossier assets doit être placé à l'intérieur de ce dossier. Je vous rappelle que lorsque vous lancez p5.js, le nom du projet par défaut est sketch, mais vous pouvez lui donner un autre nom lors de la sauvegarde de votre projet.

assets

Quand vous ouvrirez le dossier sketch, vous devrez avoir comme dans la capture d'écran ci-dessous.

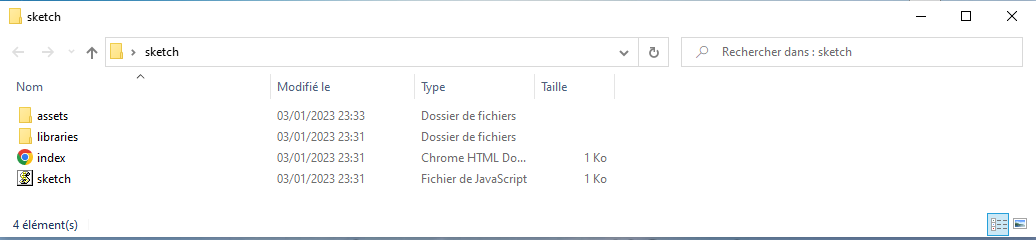
Maintenant, que vous avez le code source ci-dessus et votre dossier assets à l'intérieur du votre projet, copiez-le et collez-le dans l'éditeur de code de p5.js, puis lancez le programme en appuyant sur le bouton « flèche » en haut à gauche de votre éditeur de code. Vous pouvez tester et télécharger votre deuxième mini-jeu vidéo ci-dessous.

Mouvement de l'avion
avec vecteurs et tir basé sur
l'arc tangent et les coordonnées polaires

Avion arctan

Je vais vous fournir une explication détaillée de l'algorithme utilisé pour calculer l'angle 𝜃 entre les deux avions sur l'image ci-dessus, à l'aide de l'arc tangente. Je vais également vous présenter les algorithmes du code source pour convertir les coordonnées cartésiennes en coordonnées polaires, afin de diriger les balles de l'avion ennemi visant l'avion mère.

Deux cas de figure pour utiliser
l'arc tangent dans les trajectoires

Cas de figure n°1

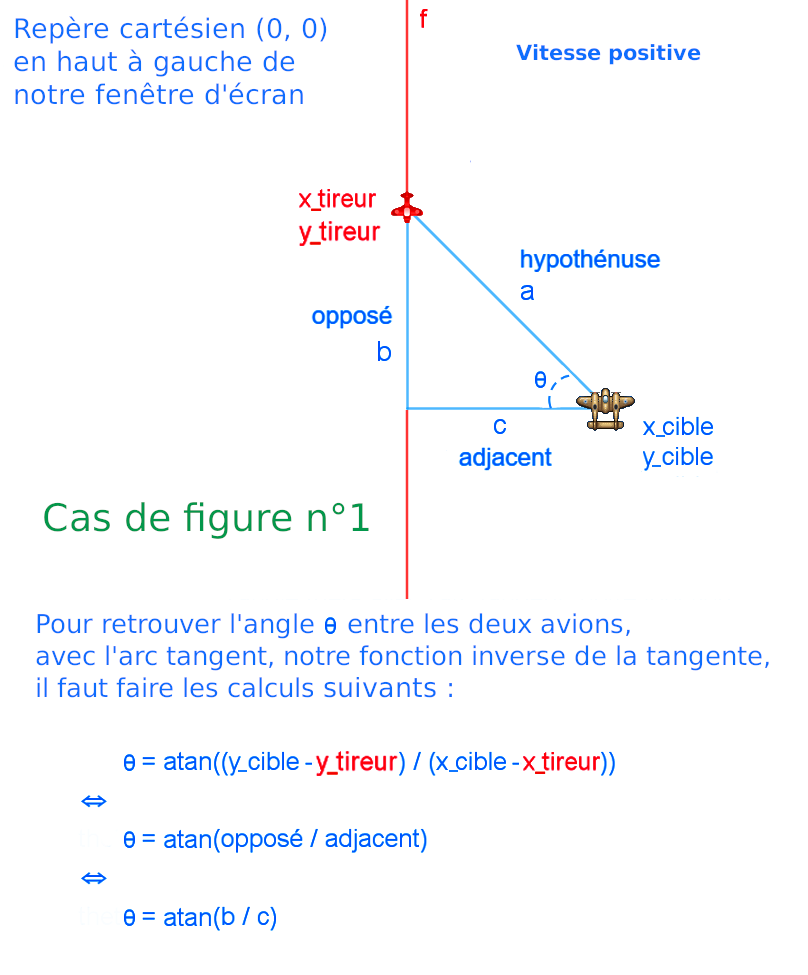
Le code ci-dessus vérifie d'abord si la variable r est égale à zéro. Si c'est le cas, il vérifie ensuite si la position x de la cible est supérieure ou égale à la position x du tireur. Si c'est le cas, il calcule l'angle de tir en utilisant l'arc tangent de la différence entre les positions y de la cible et du tireur divisée par la différence entre les positions x de la cible et du tireur. Il affecte ensuite une valeur positive tirée au hasard entre 2 et 5 à la variable vitesse. Si la position x de la cible est inférieure à la position x du tireur, il calcule de la même manière l'angle de tir et affecte une valeur négative tirée au hasard entre -2 et -5 à la variable vitesse. Ici, nous somme dans le cas de figure n° 1, la position x de la cible est supérieur à la position x du tireur et la vitesse des balles de l'avion ennemi qui vise vers l'avion mère est positive.

Cas de figure n°2

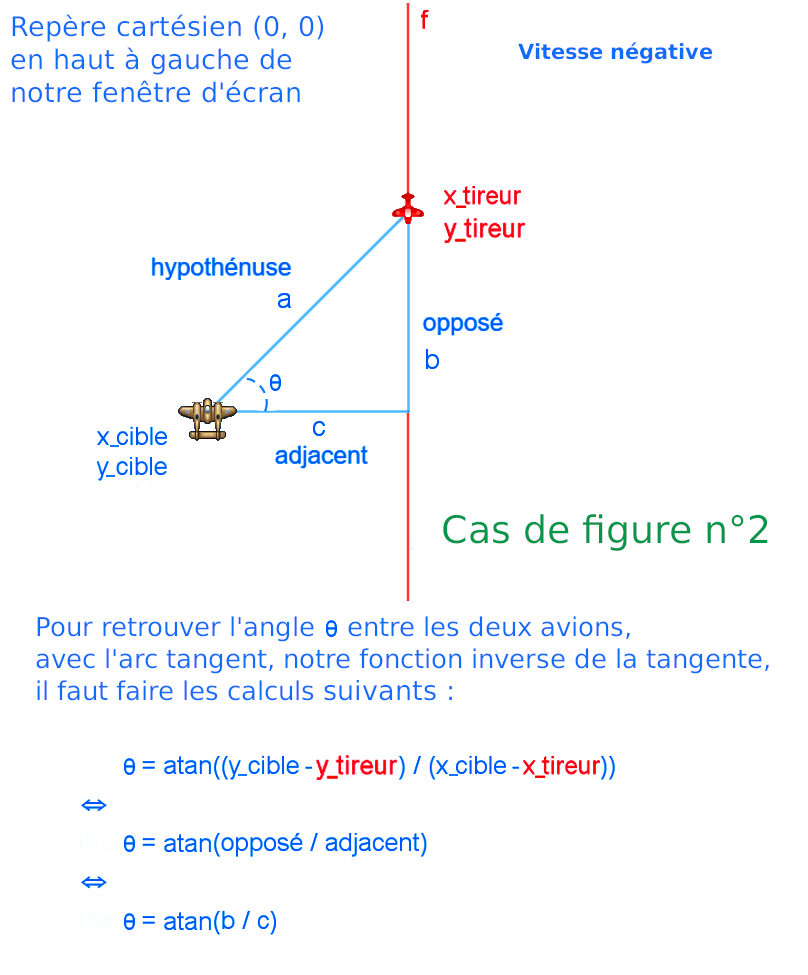
Le code ci-dessus vérifie d'abord si la variable r est égale à zéro. Si c'est le cas, il vérifie ensuite si la position x de la cible est supérieure ou égale à la position x du tireur. Si c'est le cas, il calcule l'angle de tir en utilisant l'arc tangent de la différence entre les positions y de la cible et du tireur divisée par la différence entre les positions x de la cible et du tireur. Il affecte ensuite une valeur positive tirée au hasard entre 2 et 5 à la variable vitesse. Si la position x de la cible est inférieure à la position x du tireur, il calcule de la même manière l'angle de tir et affecte une valeur négative tirée au hasard entre -2 et -5 à la variable vitesse. Ici, nous somme dans le cas de figure n° 2, la position x de la cible est inférierur à la position x du tireur et la vitesse des balles de l'avion ennemi qui vise vers l'avion mère est négative.

Deux cas de figures pour
le calcul des coordonnées polaires

Cas de figure n°1

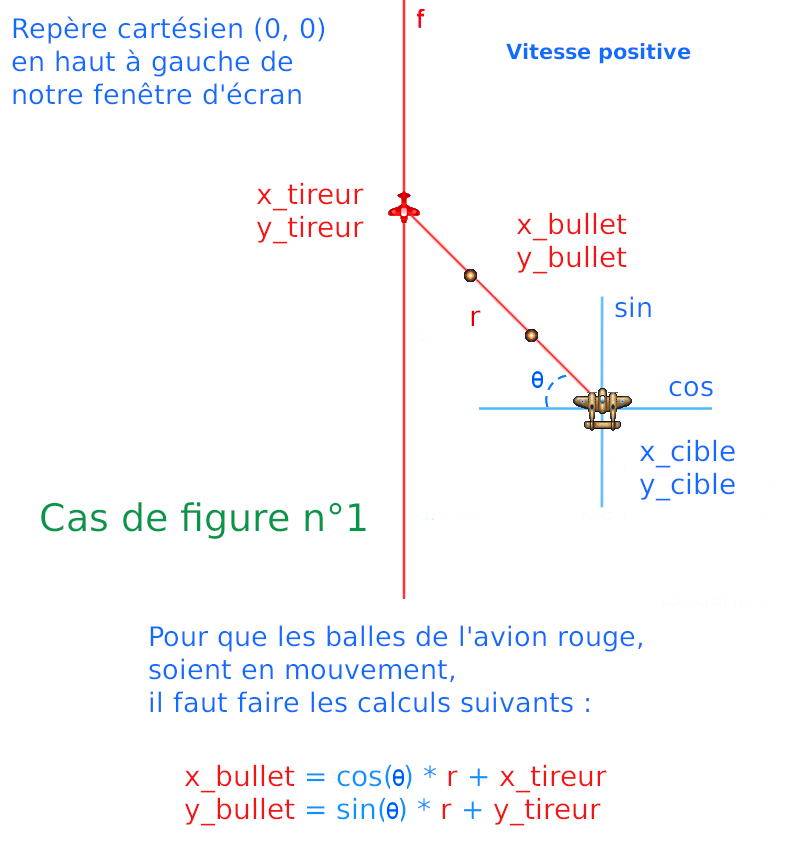
Ce code ci-dessus est utilisé pour calculer les coordonnées polaires des balles de l'avion ennemi. Il utilise les variables r, theta, x_tireur et y_tireur pour calculer les coordonnées x et y de la balle.

La variable r est incrémentée par la vitesse. Cela signifie que la distance entre le tireur et la balle augmente à chaque tour de boucle.

Ensuite, les fonctions trigonométriques cos et sin sont utilisées pour calculer les coordonnées x et y de la balle en utilisant theta (l'angle de tir) et r (la distance entre le tireur et la balle). La formule pour x_bullet est cos(theta) * r + x_tireur et la formule pour y_bullet est sin(theta) * r + y_tireur.

Finalement, les valeurs calculées pour x_bullet et y_bullet sont utilisées pour dessiner la balle à l'écran en utilisant les coordonnées x et y. Pour ce cas de figure n° 1, la vitesse est positive car x_cible est supérieur à x_tireur.

Cas de figure n°2

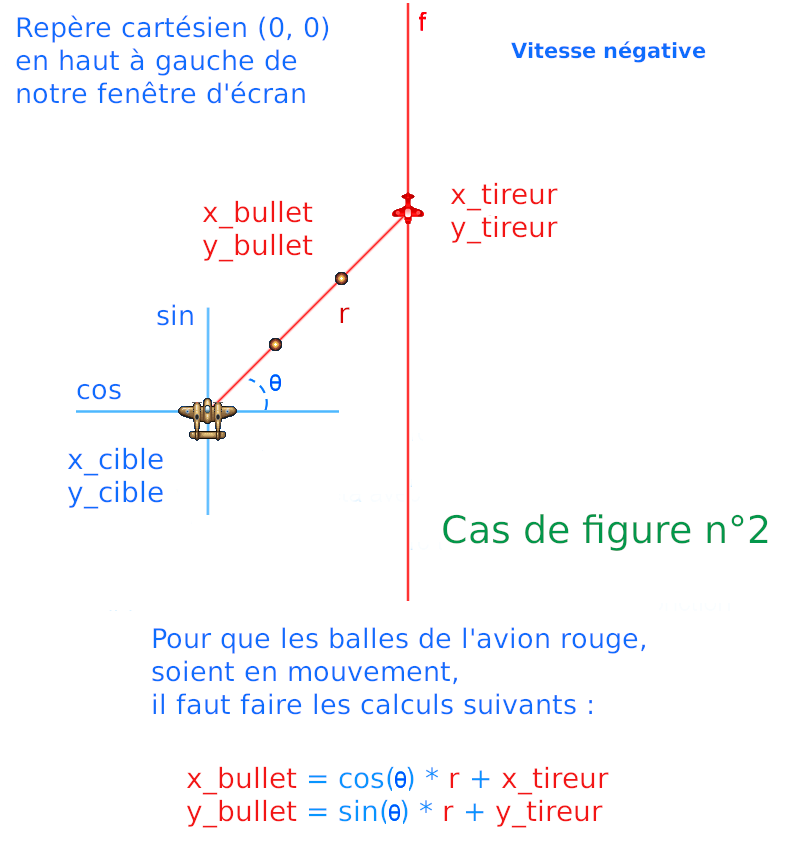
Ce code ci-dessus est utilisé pour calculer les coordonnées polaires des balles de l'avion ennemi. Il utilise les variables r, theta, x_tireur et y_tireur pour calculer les coordonnées x et y de la balle.

La variable r est incrémentée par la vitesse. Cela signifie que la distance entre le tireur et la balle augmente à chaque tour de boucle.

Ensuite, les fonctions trigonométriques cos et sin sont utilisées pour calculer les coordonnées x et y de la balle en utilisant theta (l'angle de tir) et r (la distance entre le tireur et la balle). La formule pour x_bullet est cos(theta) * r + x_tireur et la formule pour y_bullet est sin(theta) * r + y_tireur.

Finalement, les valeurs calculées pour x_bullet et y_bullet sont utilisées pour dessiner la balle à l'écran en utilisant les coordonnées x et y. Pour ce cas de figure n° 2, la vitesse est négative car x_cible est inférieur à x_tireur.

Épilogue

Voilà, nous avons terminé les algorithmes de ce deuxième mini-jeu vidéo avec nos calculs de trigonométrie. Vous pouvez maintenant passer à la suite pour notre troisième mini-jeu vidéo dans la rubrique « Algorithme » située dans la barre de menus. Le programme de ce troisième mini-jeu vidéo, qui concerne l'analyse, sera très court par rapport à nos deux premiers mini-jeux vidéo.